圆柱正弦活齿传动系统动力学特性研究

4.1引言

机械传动系统把运动和动力由动力源传递给机器执行件的工作过程中，经常会受到激振力和激振力矩的作用，从而使传动系统的零部件产生扭转振动，振动将直接影响到机械系统的精度、效率、寿命、安全性和可靠性，由此而产生的噪音也对环境产生干扰和危害。因此在设计机械传动系统时，必须考虑将振动的量级控制在一定范围内，以保证系统具有良好的动态特性。为设计高性能的圆柱正弦活齿减速器，了解该传动系统的动态特性，有必要对其进行扭振动力学分析，以便评价其振动水平，并找出影响动态特性的薄弱环节，从而为进一步动态结构优化设计、提高减速器的动态性能提供了理论依据。评价传动装置的动态性能通常有试验法和计算法两种方法。一般情况下，试验法可获得较准确的结果，但只适用于评价给定的实物或模型。而计算法通过建立动力学模型，在设计阶段就可获得评价系统动态性能所需的各种数据资料，并可根据分析结果来进行优化设计，从而在设计阶段就能得到一个具有良好动态特性的系统设计方案，因此计算方法比试验法更经济实用，但数学模型的建立具有一定的难度。
用计算方法对减速器系统进行动态分析时，其常用的数学模型有集中参数模型、分布质量模型和有限元模型三种。其中，有限元法是一种比较成熟的方法，并有现成的商用程序软件（如NASTRAN,SUPGl,I-DEAS等）可供用户使用，但它要求用户有相当高的分析与判断能力以及丰富的实践经验。该方法建立的动力学模型虽然精度较高，但只能用来分析参数固定的减速器，面对参数化的系列减速器，应用有限元法进行分析就显得非常繁琐，并且费时费力、效率低。而且在下一章的动态优化设计中需要对具有不同设计参数的减速器进行动态分析以获得训练神经网络的样本，此时有限元法就显得无能为力。因此，在本次研究过程中，采用了以集中参数模型表示的拉格朗日法，该方法基于系统能量的观点去分析系统，建立系统动力学方程，由于能量法中使用的量是标量（动能、势能、功），而不是向量（位移、力等），因而使对问题的描述更为简洁、容易和全面，且计算结果完全可以满足工程实际的需要。本章利用拉格朗日方程建立了该减速器的扭振动力学方程，计算了它的动态参数和能量分布，对减速器系统进行计算、分析和评价，找出了其薄弱环节，为进一步提高其动态特性提供了理论依据。应用Pro/ENGINEER建立起减速器的三维实体模型，利用ANSYS有限元分析软件对圆柱正弦活齿减速器的关键传动件进行了模态分析。

4.2系统扭振动力学模型的建立

为分析圆柱正弦活齿传动系统的动态特性，首先需要根据系统结构建立其动力学模型。圆柱正弦活齿传动的结构简图如图4-1所示。

根据各种零件动力学作用的不同，可把组成系统的各元件分成两类，即惯性元件和弹性元件。惯性元件指的是各轴及轴上的旋转质量，如齿轮、轴上直径较大的凸缘等盘类零件。当传动系统发生扭转振动时，它们对系统的动力学作用，主要反映在转动惯量方面，所以称之为惯性元件。弹性元件是指两惯性元件之间的轴段，它可以不计质量而只考虑扭转变形，它对振动系统的作用在于本身的扭转刚度。
建立圆柱正弦活齿减速器扭振动力学模型时，将活齿和其它质量较大而长径比较小的零件作为只有惯性而无弹性的惯性元件。把同一轴上各惯性元件的转动惯量根据实际情况，转换到该轴的两端，形成两个等效圆盘。计算两刚性圆盘之间所有轴段的扭转刚度和转动惯量，将各轴段的转动惯量迭加到该轴的两惯性元件上（一般可平均分配），各轴段的扭转刚度转换成一个弹性轴段的扭转刚度，其值应与两惯性元件之间实际轴段的扭转刚度相等。

对于图4-2a所表示的活齿与主动轴之间、活齿与导架之间、活齿与壳体之间的啮合副而言，当啮合处的弹性变形不能忽略时，可以引入一个等效的弹性轴段，视为一个弹性元件，如图4-2b所示。

根据上面叙述的方法，可以建立起如图4-3所示的动力学模型。为便于分析，将圆柱正弦活齿传动系统的动力学模型简化，由于在一个工作周期中，各活齿在扭振方向的工作状态完全相同，故可将所有的活齿等效为一个惯性元件，并根据热能不变的原则，将各活齿副的啮合刚度转化为等效的扭转刚度，然后叠加得出整体的等效扭转刚度。由此，各活齿与主动轴、导架及壳体间并联的弹性连接和阻尼分别等效为一个弹性轴段。等效简化后的动力学模型如图4-4所示。

4.3系统扭振数学模型的建立

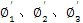
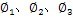
将上述模型进一步转换成链状结构。此时，需将图4-4中各轴上的刚性圆盘和弹性轴段转换到同一轴线上，构成单一轴线的等效圆盘系统的扭振动力学模型。转换时，可转换到输出轴上，也可转换到输入轴或中间任一传动轴上。转换中，按转换前后系统的动能和势能保持不变的原则。将所有参数转换到输入轴上，设 和分别为转换前后各惯性元件的扭转角，按传动比关系有：

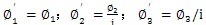
（4-1）

式中  i——减速器的传动比。

转换前系统的功能T、势能V和阻尼功D分别为：

式中   I₁——主动轴转动惯量（kg·m²）；

I_2­——活齿等效转动惯量（kg·m²）；

I₃——导架转动惯量（kg·m²)；
k_e1­——主动轴与活齿间的等效扭转刚度（N·m/rad）；
k_e2——导架与活齿间的等效扭转刚度（N·m/rad）；

k_e3——壳体与活齿间的等效扭转刚度（N·m/rad）；
C_el——主动轴与活齿间的等效扭转阻尼（N·m·s/rad）；
C_e2——导架与活齿间的等效扭转阻尼（N·m·s/rad）；
C_e3——壳体与活齿间的等效扭转阻尼（N·m·s/rad）。
根据转换前后系统的动能、势能和阻尼功保持不变的原则，将式（4-1）代入式（4-2）中，得到转换后系统的动能、势能和阻尼功分别为：

对转换成链状结构的系统，应用拉格朗日法建立系统的扭振动力学方程，系统中带有粘性阻尼，因此列出含有耗散函数的拉格朗日方程

式   L——拉格朗日函数L=T-V；

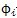
——广义坐标（i=1，2，3）；

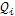
——广义力（N）（i=1，2，3）。

将式（4-3）代入拉格朗日方程（4-4）中，得到系统的动力学方程如下所示：

将式（4-5）用矩阵形式表达，则系统的动力学方程可写为：

4.4系统固有特性及势能分布率
系统固有频率以及相应主振型表现了系统的固有特性，其数值只跟系统本身的参数有关，而与其它条件无关。通过研究系统的固有特性，可对系统的动力学性能进行分析，并根据分析结果修改结构参数，以达到对结构优化设计的目的。
4.4.1系统固有频率和主振型
在分析和评价减速器系统扭振特性时，需要计算系统的各阶固有频率以及相应的主振型，这就要求解系统的无阻尼自由振动方程。当系统自由振动时，激振力矩和阻尼均为零，此时系统的动力学方程可表示为

为求解系统无阻尼自由振动方程，在微振动的情况下，方程（4-7）的解可写成如下形式：

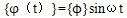
                                                   （4-8）

式中  ω——固有圆频率（rad/s)；
{ }——角位移的振幅列向量。
将式（4-8）代入式（4-7）中，并消去因子Sinωt，得到

                   （[K]-ω²[M]）{ }=0                            （4-9）

ω²和{ }又称为广义特征值和广义特征向量。由此，求解系统固有频率和主振型的问题就转化为求解方程（4-9）的广义特征值和广义特征向量的问题。

4.4.2模态柔度和势能分布率
为使设计的系统具有良好的动态特性，在建立了反映传动系统动态特性的数学模型的基础上，可对结构进行修改和优化设计。通常是要求把结构的振动强度或动柔度限制在一定的范围内。关键过程是首先找出结构的薄弱环节，然后有针对性的修改薄弱环节的局部结构，从而使整个系统的动态特性满足要求。为此需对系统的模态柔度和势能分布率进行考察。
由于系统的最大能量E_max是与振型向量{Θ}的平方成正比的，不论阻尼大小如何，这个比例关系总是一定的。因此，模态柔度是一个与阻尼无关的参数，其大小仅取决于系统的结构参数和物理参数。改变结构参数、物理参数的大小和配置方式，均将使其发生明显的变化。系统的第s阶模态柔度R^(s）的定义为

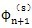
式中   ——系统末端在第s阶模态振动时的扭振幅值（rad）；

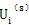
——系统中第i个弹性元件在第s阶模态振动时的热能。其值为

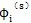
式中 ——系统中第i个弹性元件在第s阶模态振动时的转角（rad）。

模态柔度的大小表明了该阶模态的危险程度。模态柔度越大，该阶模态越危险。但并不能仅凭模态柔度值来分析造成模态危险的原因，为确定结构修改的部位和修改内容，还必须考察各个弹性元件的势能或势能分布率。势能分布率定义为

势能分布率的大小表明系统中弹性元件变形能的大小，势能分布率最大的元件也就是系统的最薄弱环节，即造成该阶模态危险的主要原因。据此可以确定相应的改进措施，以提高系统的动态性能。

4.5扭振动力学模型参数的确定

为求解圆柱正弦活齿减速器扭振动力学模型，首先要确定模型中的参数，其中包括几何参数、物理参数和外载荷参数。几何参数通过对减速器系统结构设计来确定，物理参数包括质量参数（如转动惯量）、刚度参数（如活齿副啮合刚度）和阻尼参数（如轴类零件扭转阻尼）。下面给出活齿等效转动惯量、活齿副等效扭转刚度和轴类零件扭转阻尼的计算方法。

4.5.1惯性元件的转动惯量
在圆柱正弦活齿传动中，所有活齿不仅沿圆周方向作等速旋转，同时还在轴句方向发生位移。为简化系统的动力学模型，需根据动能不变的原理，将所有活齿等效为一个惯性元件。
所有活齿的总动能：

n——活齿个数；

R——活齿在圆周方向的分布半径（mm）；

v_i——单个活齿沿轴线方向运动速度v_i=Aω₀Z₃cos（Z₃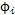 ），（mm/s）；

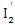
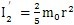
——单个活齿转动惯量 ，（kg·mm²）；

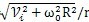
ω_zi——活齿自转角速度ω_zi= （rad/s）；

r——活齿半径（mm）；

ω₀——活齿在圆周方向的旋转角速度（rad/s）；

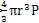
m₀——单个活齿的质量m₀= ，（kg）；

P——活齿的材料密度（kg/mm³）。

根据转换前后动能不变的原则，可列下式：

4.5.2弹性元件的扭转刚度

活齿副的啮合刚度是指工作时活齿副共同抵抗变形的能力，它与啮合副的综合弹性变形有关，在点接触的情况下，两接触体变形趋近量为

式中    F——接触点处法向作用力（N）；

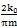
——赫兹系数；

∑P——主曲率和（1/mm）。

活齿副的啮合刚度可表示为

  

单个活齿副啮合刚度对整体刚度的贡献是角度的函数，不能简单叠加。因此需要先根据势能不变的原则，将各活齿副啮合刚度转化为等效的扭转刚度，然后叠加得出整体的等效的扭转刚度。

对于活齿与主动轴（或壳体）正弦滚道的啮合副来说，主动轴的角位移△ 在接触点作用力的方向上产生的等价线位移为

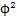
           x_i=R²△ ·sin²a_ni·cos²（u_i）                                 （4-18）

式中  a_ni——接触角（rad）；

u_i——瞬时接触线的方位角（rad）。

由啮合刚度产生的势能与转换后的扭转刚度产生的势能相等，可列方程

式中  K_i——啮合刚度（N/mm）；

n——活齿个数。

将式（4-18）代入式（4-19），整理得到等效后的扭转刚度为

同理，对于活齿与导架的啮合副来说，啮合刚度转化成等儿扭转刚度为

4.5.3轴类零件扭转阻尼

轴类零件的扭转阻尼主要是材料阻尼，根据H.H.Lin和C.Lee等的分析，其扭转阻尼可利用下式进行计算：

式中  k_s——轴类零件的扭转刚度（N·mm/rad）；

ξ_s——轴类零件的扭转阻尼系数，根据D.R.HOuser等的试验研究；

ξ_s一般取0.005～0.075；

I₁，I₂——分别为轴类零件两端惯性元件的转动惯量（kg·m·mm）。

4.6圆柱正弦活齿减速器扭振动态特性分析

初步确定圆柱正弦活齿减速器的结构参数：主动轴正弦滚道周期数Z₁=1，壳体正弦滚道周期数Z₃=4，传动比i=5，活齿半径r=4mm，正弦滚道幅值A=4mm，导架壁厚b=3mm，正弦滚道深度b₁=2mm，额定输入转速150Orpm，额定输出扭矩20N.m。利用前面建立的圆柱正弦活齿减速器系统的动力学模型对减速器系统进行扭振分析，找出系统的固有特性，即固有频率和主振型。由于轴承的旋转阻尼很小，这里忽略不计。根据减速器各元件实际尺寸及式（4-20）、（4-21）计算得到各惯性元件的等效转动惯量、弹性元件的等效扭转刚度如表4-1所示。
表4-1惯性元件的转动惯量和弹性元件的扭转刚度

根据式（4-9）、（4-10）及（4-12）计算出固有频率、势能分布率和模态柔度见表4-2。利用Matlab编制程序还绘制出图4-5所示的减速器系统的振型曲线。

表4-2圆柱正弦活齿减速器扭振动力学分析结果

通过表4-2中的分析结果我们可以看出，二阶（1539.246Hz）系统模态柔度最大，所以该阶模态是危险模态。要找出造成该阶危险模态的具体原因，我们可以考察各弹性元件的势能分布率。从表4-2中可以看到，此时3号弹性元件的势能分布率最大，这说明在扭转时，它的弹性变形能最大，即它是最薄弱环节，是造成危险模态的主要原因。从这个结论出发，便可以采取相应措施来改进设计方案。通过适当增大壳体正弦滚道与活齿间的啮合刚度来提高等效扭转刚度，便可改善该减速器的动态特性。动态性能好的系统应该是各阶模态柔度小而且每阶模态中各元件的能量分布均匀。为了达到这个目标，可以按照上述方法继续调整有关弹性元件的扭转刚度，直到获得满意的结果为止。

 

在负载变化和误差较小的情况下，圆柱正弦活齿减速器系统的激励频率就是啮合刚度的变化频率。它的计算如下：
                              ƒ=n₁/60=25Hz                              （4-23）

式中 n_i——输入轴转速（rpm)。
由表4-2中结果可知，减速器系统的一阶基频为644.357Hz，系统基频远远大于激励频率，因此该减速器的振动水平较低，振动和噪声较小。

4.7圆柱正弦活齿传动的有限元模态分析
有限元法（FEM）是一种采用计算机求解结构静、动态力学特性等问题的数值方法，它具有精度高、适应性强以及计算格式规范统一等优点，现已广泛应用于机械、航空宇航、汽车、船舶，土木、核工程及海洋工程等许多领域，成为现代机械产品设计的重要工具。当前，国际上最具影响力的有限元分析软件之一是美国ANSYS公司开发的ANSYS软件。
ANSYS软件是融结构、传热学、流体、电磁、声学、爆破分析为一体的大型通用有限元分析软件，按其功能作用可分为：一个前处理器、一个求解器、两个后处理器、几个辅助处理器等。前处理器用于生成有限元模型；求解器用于施加载荷及边界条件，完成求解运算；后处理器用于获取求解结果，以便对模型做出评价。另外，ANSYS还提供了强大的数据接口程序，使得在其他CAD软件中建立的模型可以很方便的导入ANSYS中，一旦模型成功导入后，就可以像在ANSYS中创建的模型那样对此模型进行求解运算。这些接口程序是由ANSYS公司或CAD供应商编写的软件。
其中值得注意的是ANSYS-Pro/ENGINEER接口，因为它提供了以执行部件为基础的参数化优化设计的功能。该功能允许由部件为基础的参数化Pro/ENGINEER模型开始，用ANSYS程序对其进行优化，并以一个优化的Pro/ENGINEER模型结束，且仍是以部件为基础的参数化模型。

4.7.1减速器三维实体模型的建立
进行有限元分析前首先必须建立减速器的三维实体模型。虽然ANSYS在有限元分析方面具有强大的功能，但是在三维实体建模方面并不比专业的CAD软件占有优势。对于复杂的实体模型，甚至需借助其它软件才能完成。

工程用三维实体建模软件主要有Pro/ENGINEER、Ideas、UG等。其中美国PTC公司开发的Pro/ENGINEER是世界上第一个基于特征的参数化实体建模软件，其在三维建模、尤其是复杂曲面的造型方面处于国际领先水平。考虑到圆柱正弦活齿减速器中，主动轴及壳体等零件的实体特征比较复杂，因此本文采用Pro/ENGINEER对减速器进行三维实体建模。
在进行有限元分析时，我们将螺栓、端盖等辅助零件予以忽略，而只关注与减速器工作直接相关的主动轴、活齿、导架和壳体等关键零件，据此建立减速器三维实体模型如图4-6所示。

4.7.2主动轴及导架的模态分析
在结构动力学分析中，模态分析用于确定所设计的结构或机器部件的振动特性（固有频率和振型）。由于主动轴和导架动力学特性直接影响减速器的性能及寿命，所以应对主动轴、导架进行模态分析，确定其固有频率及振型，也为谱响应分析、随机振动分析创造条件。
零件模型采用IGES格式导入ANSYS，对于结构中含有复杂曲面的模型，Pro/E和ANSYS中定义的拓扑结构也不尽相同，若直接将在Pro/E中输出的IGES格式实体模型导入ANSYS，会致使网格划分耗费大量时间，甚至导致无法对模型划分网格。因此，本文在Pro/E中仅将模型的表面以IGES格式输出，在导入ANSYS后，应用VA命令将零件表面重新生成实体。值得注意的是，生成体之前，应采用AGLUE命令检查面与面交界的连续性，否则将不能成功生成实体模型。
拓扑修补后选择单元为solid45，指定杨氏模量为2.06×10¹¹N/m²，密度为7800kg/m²，泊松比为0.3。对模型采用人工网格划分，利用LESIZE来控制网格密度，考虑到主动轴空间正弦滚道的结构特点，分割正弦滚道边界曲线和正弦滚道的三条拓扑线，并使线分割的密度相同。对于导架，分割活齿槽的直边，并使线分割的密度相同。
四面体单元每个节点有三个自由度（Tx,Ty,Tz)，通过限制节点的自由度，对模型施加约束。模拟轴承的作用，在安装轴承处的零件表面施加约束，首先将表面上所有节点的坐标由笛卡尔坐标（x,y,z）转换为柱坐标（R,θ,Z)，然后限制自由度R。并在主动轴的输入轴端面和导架的输出轴端面，限制所有节点的自由度。划分网格并施加约束的主动轴见图4-7。

选择Subspace特征值求解器，指定扩展模态数为4，频率范围为0～1000Hz。求得输入轴的前四阶固有频率为101.SHz、207.2Hz、660.6Hz、661.2Hz，对应的振型见图4-8。一阶振型为绕z轴扭转，二阶振型为沿z轴轴向拉伸，三阶振型为在xoz平面弯曲，四阶振型为在yoz平面弯曲。

同样划分网格并施加约束的输出轴见图4-9。求得输出轴的前四阶固有频率为82.2Hz、265.4Hz、386.2Hz、386.7比，对应的各振型见图4-10。一阶振型为绕z轴扭转，二阶振型为沿z轴轴向拉伸，三阶振型为在xoz平面弯曲，四阶振型为在yoz平面弯曲。

根据旋转轴转速与频率的关系：

                                 n=60·ƒ                                （4-24）

式中  n——转速（rpm）；

ƒ——频率（Hz）。

将主动轴、导架的固有频率转化为临界转速，所得结果见表4-3。

表4-3 主动轴、导架的临界转速        （rpm）

输入轴和输出的工作转速分别为1440rpm和288rpm，从表4-3中可以看出，两轴的工作转速均大在低于临界转速。

4.8本章小结

1.将圆柱正弦活齿减速器的各个零件简化成相应的惯性元件和弹性元件，建立减速器的系统动力学模型：利用拉格朗日方程从系统能量的角度建立了减速器系统的动力学数学模型；并给出了活齿等效转动惯量、啮合副等效扭转刚度和轴类零件阻尼的计算公式；

2.根据建立的动力学模型，通过编程求解圆柱正弦活齿减速器系统的无阻尼自由振动方程，得到了该系统的固有频率、模态柔度和各阶振型等固有动态特性参数。结果表明，该减速器具有良好的动态特性；

3.根据所求的模态柔度和各弹性元件的势能分布率，找到了危险模态及导致危险的薄弱环节，为进一步改进其结桅杆，提高动态特性，提供了理论依据；

4.应用Pro/ENGINEER建立起减速器的三维实体模型，利用有限元分析软件ANSYS对样机中的关键件进行了模态分析。