(2)综合不对中180°位置:当圆环上的单元体旋转到最左端时,也就是180°位置时,单元体的应力如下图所示
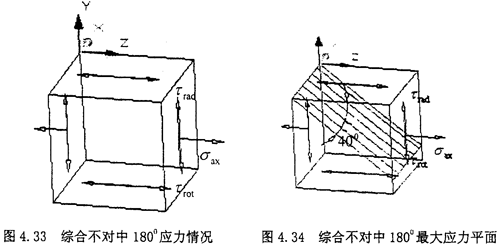
此时的受力仍然属于两向应力状态,因为径向不对中产生的剪应力方向和扭转产生的剪应力的方向在同一平面上而且相互平行。根据计算可以知道
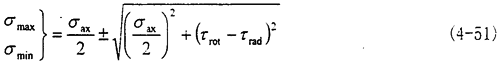
此时主平面上的正应力平面的角度有这种关系

(3)综合不对中270°位置:当圆环上的单元体旋转到最下方时,也就是270°位置时,单元体的应力如下图所示
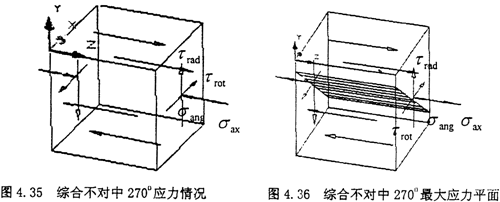
此时的应力情况属于三向应力状态,所以其分析过程和径向不对中90°以及270°情况相似,只是这里还有了附加的轴向拉应力和附加的角向应力,将各个应力值

将上述主应力的值代入就可以得知
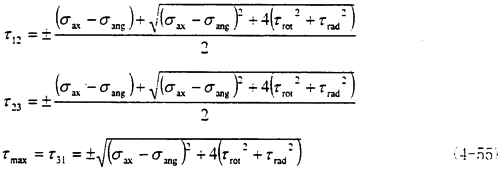
这时取σax=10.6MPa,τrad=10MPa,σang=10.6MPa,代入式(4-49)中,可以得出最大主应力为σmax=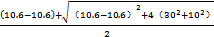 =31.6MPa
=31.6MPa
(4)综合不对中360°位置:当圆环上的单元体旋转到最右端时,也就是360°位置时,单元体的应力如下图所示
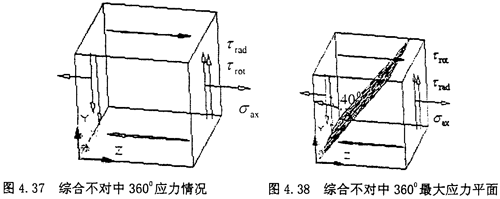
此时的受力仍然属于两向应力状态,
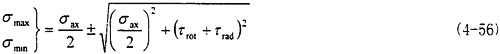
此时主平面上的正应力平面的角度有这种关系

这时取σax=10.6MPa,τrad=10MPa,代入式(4-56)中,可以得出最大主应力值为
σmax=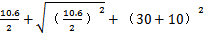 =45.65MPa
=45.65MPa
现在比较一下四个不同位置时的最大主应力的大小

根据上面的分析,可以知道联轴器在综合受力的情况下,其总的应力情况与四个量有关,也就是σax、τrad、σang与τrot的叠加。为了能够更加形象直观地描述由于不对中量产生的附加应力与总应力的关系,下面进行曲线的拟合。考虑到σax与σang方向都在同一直线上,而τrad与τrot的方向也在一条直线上,但是这两条直线相互垂直。所以以σ为横坐标轴,τ为纵坐标轴建立坐标系后。各个不对中量都有一个范围,因而由不对中量引的附加应力也有一个范围,

综合以后可知,附加应力的在一个大的矩形里面变化。见图4.39。矩形的方程由下面两式决定:
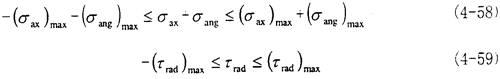
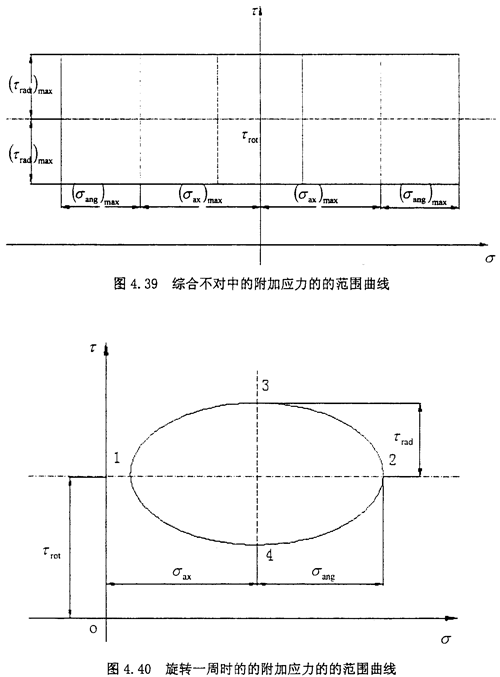
而在联轴器旋转一周的过程中,各个不对中量都是定值,此时应力范围在见图4.40的椭圆。该椭圆的方程为
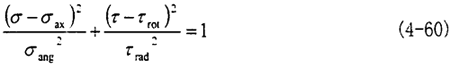
4.7 本章小结
本章主要从力学的角度对联轴器进行各种不对中的分析。从联轴器各种不对中的分析结果可以得出以下结论。
1.在轴向不对中时,在给定的轴向不中量情况下,有最大主应力为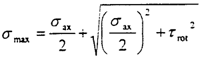 最大应力方向随着旋转角变化。
最大应力方向随着旋转角变化。
2.在径向不对中时,在给定的径向不中量情况下,最大主应力为发生在联轴器360°位置,有σmax=+(τrot+τrad)。最大主应力平面方向与y轴成45°夹角。即360°位置为径向不对中时的危险点。
3.在角向不对中时,在给定的角向不中量情况下,最大主应力发生在90°位置,
 。即900位置为角向不对中时的危险点。
。即900位置为角向不对中时的危险点。
4.在综合不对中时,在给定的轴向、径向和角向不中量的情况下,最大应力为发生在联轴器90°位置,即有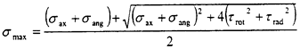 最大危险点在90°位置。
最大危险点在90°位置。
随后根据上述结论进行了不对中量范围的讨论。最后得出了用一个大的矩形来表示由于不对中产生的附加应力的范围。矩形的形状由下面的两个式子来决定:

最后根据实际情况的不对中量,绘出了联轴器在旋转一周的过程中最大应力的椭圆。该椭圆的方程为
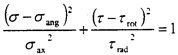 。
。
上一页
下一页


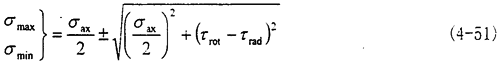



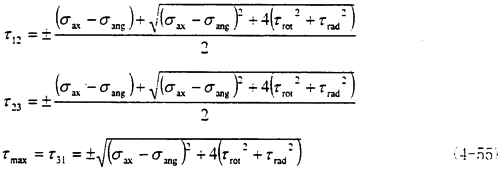

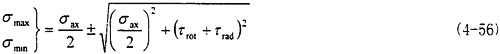


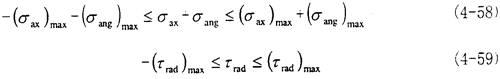

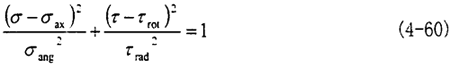
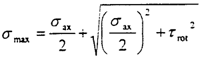 最大应力方向随着旋转角变化。
最大应力方向随着旋转角变化。 。即900位置为角向不对中时的危险点。
。即900位置为角向不对中时的危险点。
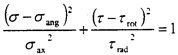 。
。