4.4.3 仿真结果分析
由图4-9可以知道,当输入轴转速恒定为90o/s时,输出轴并不作恒速转动,而是以90o/s为中心,作非常有规律的周期性运动,在每一个回转周期中,它的变化频率为3次。这里的结果同第三章中的曲线图3-8也是完全吻合的,因此在一定的程度上也证明了三叉杆万向联轴器转速分析理论的正确性。
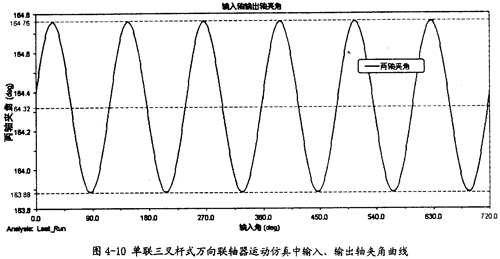
由图4-10可以知道,输入轴同输出轴的夹角在三叉杆式万向联轴器运转时是不断变化的,在每一个回转周期中,它的变化频率为3次,这证明了这种联轴器是一种非定心式万向联轴器,同时在一定的程度上验证了三叉杆式三轴颈的交点以三倍于万向联轴器的转速作圆周运动的理论的正确性。另外还可看出尽管夹角在不断变化,但变化非常小,对两轴的夹角大小影响很小,本次仿真中夹角大小平均是164.32°(其补角为15.7°,即是第三章中理论计算中的角度之一)。
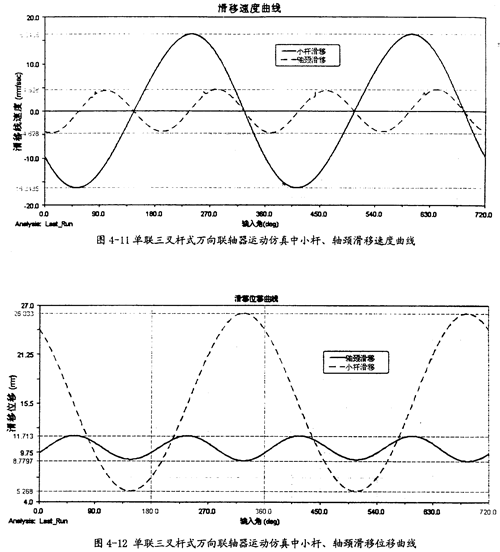
由图4-11可以知道,在一定的夹角下,小杆在滑道中的滑移速度同小杆球面中心相对轴颈的滑移速度是不同的,前者要远大于后者,且它们变动的频率也不一样,在一个回转周期中,前者频率是1次,而后者是2次。此图中的两曲线同第三章中的理论分析曲线图3-11、图3-12是吻合的,只是小杆滑移的速度曲线在外形上有一点差异,仿真的曲线相当的平滑、规则,但理论分析曲线却不规则,这可能是在计算中简化和省略的原因。尽管如此,这也证明了三叉杆式万向联轴器理论分析中对小杆滑移速度和轴颈滑移速度这两项计算的正确性。
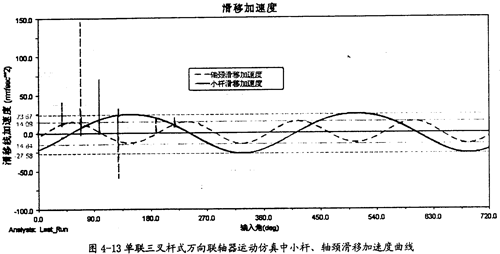
由图4-12可以知道,在一定的夹角下,小杆在滑道中的滑移位移同小杆球面中心相对轴颈的滑移位移是不同的,前者(20.76mm)要远大于后者(2.93mm),且它们变动的频率也不一样,在一个回转周期中,前者步率是1次,而后者2次。此图中的两曲线同第三章中的理论分析曲线图3-9、图3-10是吻合的。这在一定的程度上也证明了三叉杆式万向联轴器理论分析中对小杆滑移位移和轴颈滑移位移这两项计算的正确性。
由图4-13可以知道,在一定的夹角下,小杆在滑道中有滑移加速度同小杆球面中心相对轴颈的滑移加速度是不同的,前者要大于后者,且它们变动的频率也不一样,在一个回转周期中,前频率是1次,而后者2次。此图中的两曲线同第三章中的理论分析曲线图3-13、图3-14是吻合的,只是小杆滑移的加速度曲线在外形上有差异,仿真的曲线相当的平滑、规则,但理论分析曲线却不规则,这可能是在计算中简化和省略的原因。尽管如下,这在一定的程度上也证明了三叉杆式万向联轴器理论分析中对小杆滑移加速度和轴颈滑移加速度这两项计算的正确性。(值得说明的是此图中曲线有时有突变的现象,主要是考虑到计算机的性能,计算中步长稍大的原故。在后面的分析曲线中也出现了这样的情况,将不再作说明。)
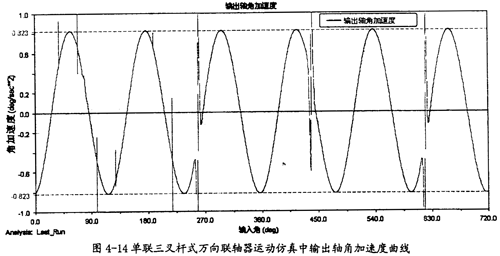
由图4-14可以看出,由于输出轴角速度的波动,其角加速度也是在不断变化,当两轴夹角在15.7°时,这种波动的幅度也是相当小,这证明由角加速度引起的附加扭矩非常小,这样的结果是这种联轴器在传动中运转应该是较为平稳的。
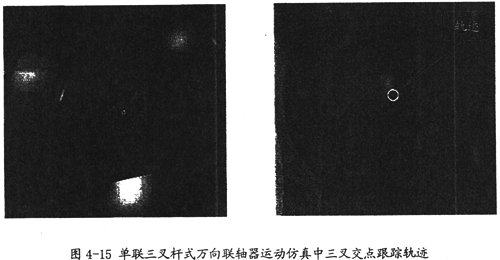
由图4-15可以看出,在单联三叉杆式万向联轴器的运动仿真中,三叉交点运动轨迹是一个圆,相对于半径值R(此值的意义见第三章)它的半径是相当小的,这也解释了为何运动中两轴夹角在不断作微小的变化,同时也证明了轴头中心轨迹理论的正确性。
4.4.4 结论
通过以上的结果分析,可以确定的说,单联三叉杆式万向联轴器的理论分析结果和其计算机仿真的结果可以相互验证,这在一定的程度上说明以前的理论分析是正确的。
4.5 双联三叉杆式万向联轴器的运动仿真
4.5.1 仿真模型的建立
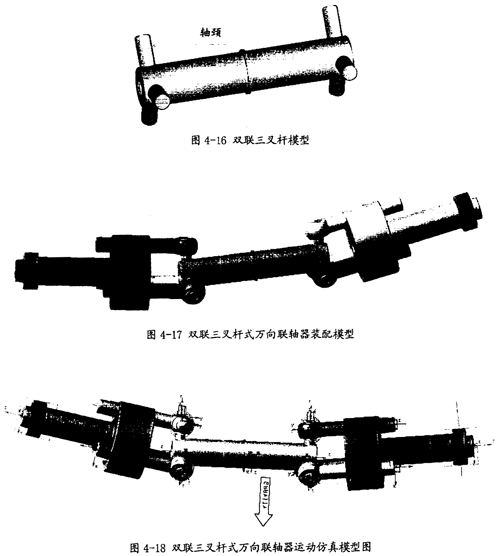
在本次分析中,建立的装配模型是在第三章中图3-2所示的模型的基础上除去关节轴承,将三叉杆用图4-16所示的双联三叉杆替换,在此模型的右端再加上同左端相同的结构,就得到双联三叉杆式万向联轴器的装配模型。此模型如图4-17所示。
在这个装配模型的基础上通过添加运动副和运动驱动构成图4-18所示的运动仿真模型。添加的运动副和运动驱动如下:
在滑杆套轴和左支承间添加旋转副;
在小杆同滑杆套轴间添加移动副(本来圆柱副也可,这里是局部自由度);
在内球头同小杆之间添加球面副;
在内球头同双联三叉杆轴颈之间添加圆柱副;
在旋转副上添加恒速驱动,大小为90o/s。
通过模型检验,可知模型中:
有15个移动件、6个圆柱副、2个旋转副、6个球面副、6个移动副、1个驱动、模型共有7个自由度。
在此模型中将重力加速度设为O,即仿真是在无重力的环境下进行的。
上一页
下一页






