4.5.2  运动仿真

设定一定的步长，对模型进行仿真分析，并输出如下测量结果的曲线：

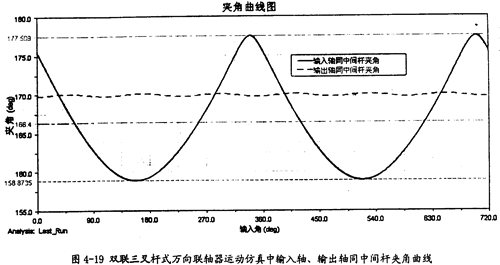
输入轴、输出轴同双联三叉杆（又称中间杆）夹角曲线（如图4-19）；

中间杆同输出轴夹角曲线放大图（如图4-20）；

输入、输出轴角速度曲线（如图4-21)；

小杆和轴颈滑移位移曲线（如图4-22)；

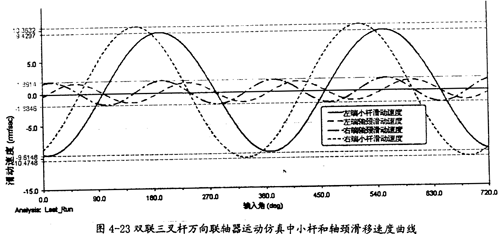
小杆和轴颈滑移速度曲线（如图4-23)；

双联三叉杆轴颈轴线交点（简称三叉交点）的运动轨迹（如图4-24）。

4.5.3  仿真结果分析

由图4-19可以看出，双联三叉杆式万向联轴器在转动的过程中，中间杆同输入轴、输出轴之间的夹角都在变化，且两个夹角的变化的大小相差很大，一个较为平滑（β=10°)，而另-个则以较大的幅度（18°）呈周期变化，在每一个回转周期中，它的变化频率为l次。

由图4-20可以看出，中间杆同输出轴间的夹角变化也呈现一定的规律，在每-个回转周期中，它的变化频率为3次。结合图4-19、图4-20可知中间杆同输入轴及输出轴夹角的变化频率是不-样的，这是双联三叉杆式万向联轴器有别于单联三叉杆式万向联轴器的一种特性。

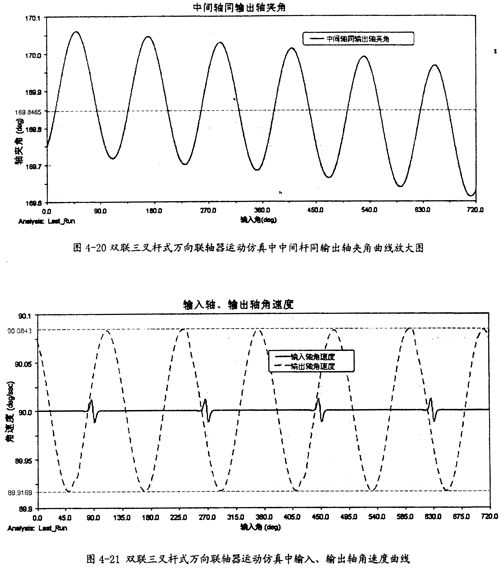
由图4-21可以看出，双联三叉杆式万向联轴器同单联三叉杆式万向联轴器的输出曲线相似，当输入轴转速恒定时，输出轴转速呈现有规律的波动，在每一个回转周期中，它的变化频率为3次，同图3-8中的β=10°时的曲线相比，双联同单联的情况差不多，故三叉杆式万向联轴器在双联的结构形式下输出转速特性直观上无改善。

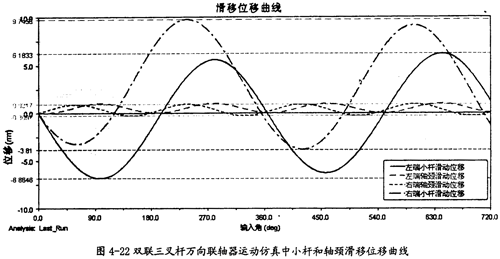
由图4-22可以看出，双联三叉杆式万向联轴器在运转的过程中，左右两端的小杆滑移位移量几乎相等，左右两端轴颈的滑移位移量也接近等值，且轴颈的滑移位移量比小杆沿滑道滑动的位移量要小得多，这同单联三叉杆式万向联轴器的特性是相同的。

由图4-23可以看出，双联三叉杆式万向联轴器在运转的过程中，左右两端的小杆滑移速度几乎相等，左右两端轴颈的滑移速度也接近等值，且轴颈的滑移速度比小杆沿滑道滑移速度要小得多，它们的变化频率同单联时的情况相比也无变化，在大小上同β＝10°的单联三叉杆式万向联轴器的特性是相同的。

由图4-24可以看出，双联三叉杆式万向联轴器在运转的过程中，双联三叉杆的左右两端三叉交点的运动轨迹都呈螺旋线变化，且非常有规律，它们的正面视图均为标准的圆，这一种特性有别于单联的三叉杆式万向联轴器的特性。这种情况的出现主要是由于中间杆在转动的过程中是一种准圆锥摆运动（由于中间杆同输入轴及输出轴夹角变化不一样，如图4-19所示）,而且因为系统的自由度不为0，系统实际进行的是动力仿真，于是产生了同中间杆轴线不垂直的离心力，这样在中间杆的轴向上就会有分量，在此分力的作用下必定会出现中间杆向一端的运动。（因为中间杆在轴向上可以自由运动，故在实际的应用中，如果重力在中间杆的轴向上有分量，那么中间杆也会移向一端。这样的情况并不是我们所想要的，所以要想在实际中应用双联的三叉杆式万向联轴器就必须对这种结构进行改进。）

4.5.4  结论

由以上分析可知，三叉杆式万向联轴器在单联和双联时的运动特性，在夹角变化的规律上和三叉交点的运动轨迹上有根本性的改变，而在本章所测试的其它特性中几乎无变化。

4.5  本章小结

本章开始介绍了虚拟样机技术及其在计算机上实现的软件ADAMS，并利用三维建模软件Pro/E联合ADAMS进行运动仿真，在验证这种方案可行性的基础上，分别对单联三叉杆万向联轴器和双联三叉杆万向联轴器进行了运动仿真分析。通过分析、比较，得出如下结论：

单联三叉杆式万向联轴器的理论运动分析结果同仿真分析结果是吻合的；

单联三叉杆式万向联轴器同双联三叉杆式万向联轴器的运动规律有的发生了改变，有的保持不变，特别是输出轴的转速特性在双联时同单联时几乎无变化。

上一页

下一页