5.3.1.2 模型的检验
建立好模型后,对模型进行检验,结果如下:
模型中共有15个构件;
有6个圆柱副,2个旋转副,6个球面副,6个移动副;
模型共有8个自由度(Gruebler数),且每个约束均为必要,无冗余;(此过程显示非常重要,如果检验中有冗余的约束,则在求解的过程中,ADAMS会除去这些约束,但除去这些约束在那个运动副上是不可控制的,那样的后果是在动力仿真中中得到的运动副上的反作用力就不正确,只能通过在柔性体的动力仿真中才可加以补救。此模型中约束正好无冗余,这样在每个运动副中所测量的反力都应是正确的。)
在模型的两端加有两个力矩,一个用作主动力矩另一个则用作被动力矩;
在每个运动副中均有摩擦,共施加20个摩擦力。
5.3.2 动力仿真
通过设定一定的仿真步数,选用一种适合于刚性系统(特征值变化大的系统),且积分稳定性好的求解器(本次仿真选用了MODIFIED求解器。因为在ADAMS提供的GEAR,DASSL,MODIFIED,ABAM,SI2这五种求解器中,GEAR、DASSL、MODI FIED求解器适合于刚性系统,且积分稳定性的关系为:MODIFIED>DASSL>GEAR。),进行动力仿真,并输出如下测量结果:
STEP函数的变化曲线(如图5-7所示);
输入轴转角的变化曲线(如图5-7所示);
输入轴角速度的变化曲线(如图5-7所示);
小杆受力曲线(如图5-8所示);
轴颈受力曲线(如图5-9所示):
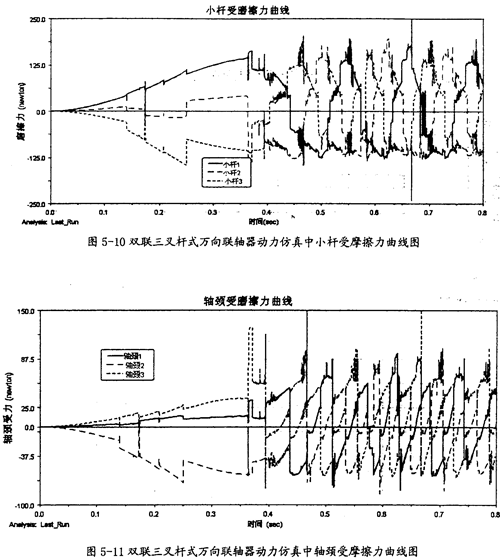
小杆受摩擦力曲线(如图5-10所示);
轴颈受摩擦力曲线(如图5-11所示);
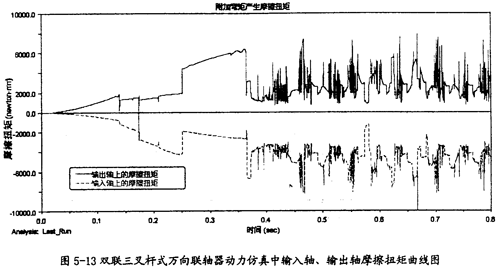
输入轴、输出轴由附加弯矩产生的摩擦扭矩(如图5-12所示)。
以上所有的测量结果均是在同-次仿真中得到,仿真历时0.8秒,双联三叉杆式万向联轴器在仿真中经历了从启动到平稳波动的动态过程。在所有力的测量曲线中,曲线有突变现象,这-现象可能同模型中的刚体假设,以及静摩擦系数到动摩擦系数和突变有关,如果用柔性体代替刚体,其结果应该会平滑。但总的来说,这里的曲线在-定的程度上反应了这些力的变化趋势,也可以作为分析的参考。

5.4 仿真结果分析
由图5-7可以看出,双联三叉杆万向联轴器在动力仿真的过程中,输入力矩逐步以STEP函数的趋势增大,当其克服静摩擦力后,开始转动,在角速度达到一定的值后,出现波动的现象(红色线条所示),并非如平常想象的近似等速转动。

由图5-8可以看出,双联三叉杆式万向联轴器在动力仿真的过程中,一端的三个小杆在移动副中受到的力逐步增加,当系统开始转动后,它们受到的力呈现有规律的波动,但互相之间有一个相位差。正是由于它们的受力变动复杂,故它们在滑杆套轴上的三个反力的向量和就可能不为0,这样的结果是,它们除了在滑杆套轴(输入轴)上形成负载扭矩外,还会产生附加弯矩的作用。
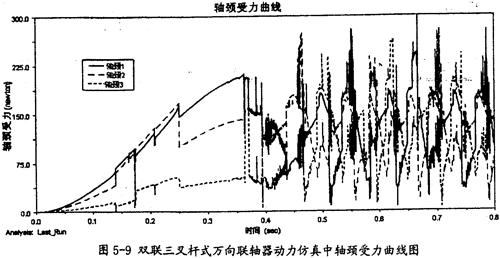
由图5-9可以看出,双联三叉杆式万向联轴器在动力仿真的过程中, 双联三叉杆一端的三轴颈同内球头的圆柱副上的作用力变化趋势同图5-8中的小杆变化趋势是相同的。由于它们的受力变动复杂,故这三力在双联三叉杆一端上的向量和也可能不为0。这样在双联三叉杆上也会产生附加弯矩的作用。而且轴颈受力平均较小杆的受力要大。
由图5-10可以看出,双联三叉杆式万向联轴器在动力仿真的过程中,其一端的三小杆同滑杆套轴间的摩擦力变化相当有规律。当小杆相对滑杆套轴运动反向时,它们就会在正负间有规律的切换。
由图5-11可以看出,双取三叉杆式万向联轴器在动力仿真的过程中,其一端的三内球头同轴颈间的摩擦力变化相当有规律。当内球头相对轴颈运动反向时,它们就会在正负间有规律的切换。但在这里产生摩擦力的平均大小要较小杆上的小得多。
由图5-12可以看出,双联三叉杆式万向联轴器在动力仿真的过程中,其一端的三个小杆所受的摩擦力的合力变动较有规律,其值在开始一段平滑,其后几乎以0为中心波动。由于这三个摩擦力的方向均平行于输入轴或输出轴轴线,故此合力会在输入轴和轴出轴上产生轴向的力,在输入轴和输出轴上产生摩擦扭矩。如取其水平较高值60牛来计算,它产生的摩擦扭矩为270N·mm(60×0.3×15=270,其中0.3为动摩擦系数,15为摩擦半径),此值相对图5-13中的值而言相当小。

由图5-13可以看出,双联三叉杆式万向联轴器在动力仿真的过程中,输入轴和输出轴上的摩擦扭矩逐渐增加,然后开始一种复杂的波动。由于本次仿真是在无重力的环境下进行的,因此,不会因为重力的作用在输入轴和输出轴上产生弯矩和由其产生的反作用力而形成弯矩,当然也就没有它的作用而形成的摩擦扭矩,则只有可能是三小杆同滑杆套轴间的作用力而导致在滑杆套轴上产生的轴向力和弯矩而产生此摩擦扭矩,但由图5-12的分析可知,轴向力产生的摩擦扭矩很小, 则可以证明滑杆套轴上有较大的附加弯矩存在,而且它是形成摩擦扭矩的主要原因。
5.5 本章小结
本章中阐述了机械动力学的几种分析方法,明确了动力分析方法的趋势。并在多刚体动力学的理论基础上,利用目前最为流行的多体动力学软件ADAMS,对双联三叉杆万向联轴器进行了动力学模型的建立和动力仿真,得到了许多可视化的结果。证明这种联轴器在传动中其受力相当的复杂,并得出了一些定性的结论,这种联轴器的进一步研究开发打下了基础。
上一页
下一页






