第6章 三叉杆式万向联轴器的振动分析
6.1 引言
万向联轴器是一种典型的回转机械，而对回转机械的转子无论静平衡做得如何好，仍会有不平衡惯性力存在，激发机械系统产生振动。三叉杆滑移式万向联轴器输入轴以恒定角速度转动时，由前面分析可知输出轴的转速和承受的扭矩均作微小的周期性变化，同时在输入轴上还有周期变化的弯矩，因此系统在这种周期性的激励下振动的产生是必然的。而对于联轴器这种结构系统来说，不希望有过大的振动发生，因为振动会造成结构的共振和结构疲劳而使结构破坏；还可能在系统中往往产生很大的扭转附加载荷，不仅使系统中零部件发生断裂，同时还会使系统向外界发出噪声，严重影响系统的可靠性和耐久性。同时还将引起其它系统的振动和噪声，从而影响整个系统的性能。
故而，正确、有效地确定共振频率，尽可能避开共振区运行（很多情况不一定能避开，那就需要改进设计），对设备的设计、安装、使用、维护有重要意义。
6.2 振动分析采用的一般方法
对于结构系统的振动分析，目前的计算方法主要有经验公式法，传递矩阵法，有限元法等多种方法。
经验公式法——经验公式法是对某些成型的结构列出其经验公式，通过这种公式对结构的固有频率进行计算。这种方法适用范围非常有限。
传递矩阵法——传递矩阵法是将一个连续系统离散化为一系列相互连接的子系统，根据所要研究的问题，选取一系列的状态向量，各个相互连接的子系统之间的关系可以通过由这些状态向量组成的传递矩阵表示，这样从起点推算到终点，再根据边界条件得到系统的频率方程，表示，这样从起点推算到终点，再根据边界条件得到系统的频率方程，即可得到系统的固有频率和模态向量。
有限元法——有限元法是一种数值计算方法。它的基本思想是将问题的求解域划分为一系列的单元，采用单元体对连续弹性体进行简化，但质量和弹性是分布的，不是集中的，单元之间仅靠节点相连。单元内部的待求量可由单元节点间通过选定的函数关系插值得到。由于单元形状简单，易于用平衡关系和能量关系建立节点间的方程式，然后将各单元方程集组成总体代数方程组，计入边界条件后可对方程求解，得到物体的运动特性。现阶段由于CAD、CAE软件的日益成熟，以及电脑硬件性能的大大改善，这种方法已成为一种流行的分析方法。
6.3 本章分析采用的方法
本章分析采用的是基于虚拟样机技术进行的传动系统振动分析，其实质是有限元方法，即通过对各构件的模态进行模态叠加和模态综合而得到系统的固有频率和振型。
其简要的步骤是如下：
首先通过CAD软件（Pro／E）建立双联三叉杆式万向联轴器的零件模型和装配模型；
接着运用有限元分析软件ANSYS建立了各零件的有限元模型，获取模态并生成柔性体描述文件——模态中性文件（MNF文件）；
然后在ADAMS中建立双联三叉杆万向联轴器的刚性体模型，再利用上一步生成的MNF文件，生成系统各构件的柔性体，将柔性体取代相应的刚体，得到系统的柔性体模型；
最后在ADAMS中，利用ADAMS的振动分析模块ADAMS/Vibration完成整个系统的振动特性的分析。
6.4 振动分析的理论背景
6.4.1 有限元软件ANSYS简介
一般机械系统的几何结构相当复杂，受的负载也相当多，理论分析往往无法进行。想要解答，必须先简化结构，采用数值模拟方法分析。由于计算机行业的发展，相应的工程分析软件也应运而生，有限元软件ANSYS就是其中之一目前ANSYS软件在工程上应用相当广泛，如机械、电机、土木、电子及航空等领域都有大量的使用。而且它能达到某种程度的可信度，颇获各界好评。使用该软件，能够降低设计成本，缩短设计时间。
以ANSYS为代表的工程数值模拟软件，是一个多用途的有限元法分析软件，可用来求解结构、流体、电力、电磁场及碰撞等问题。它包含了前置处理、解题程序以及后置处理。将有限元分析、计算机图形学和优化技术相结合，已成为现代工程学问题必不可少的有力工具。
6.4.2 MNF文件
模态中性文件期——MNF文件，是柔性体描述文件，该文件中包含了柔性体的几何信息（包括节点的位置及其连接）、节点的质量同转动惯量、各阶模态、模态的广义质量和广义刚度等信息。在有限元软件ANSYS中就可以生成此文件。利用此文件可以在多体动力学软件ADAMS中生成刚体的柔性体模型。此文件仅适用于线性结构受力行为。
6.4.3 模态叠加
模态叠加法是建立在模态的正交性及展开定理的基础上的一种求解动力响应的近似方法。ADAMS之所以能够根据不同的外力状态适时反应出正确的变形结果，正是利用了“模态叠加（Modal Superposition）理论”，由有限元分析（FEA)计算出特征值、特征向量、和模态，再由模态叠加关系式，即可计算得到各点的变形量。其具体理论如下：
一个具有N个自由度的系统的强迫振动方程为：
[M]{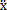
}+[C]{
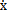}+[K]{x}={f}
其中：
{x}——位移向量 [M]——质量矩阵
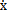{}——速度向量 [c]——阻尼矩阵
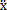{}——加速度向量 [K]——刚度矩阵
{f}——激励力向量
对于一般的已知激励力，运用数值计算方法总是可以解出响应来的。然而，对于大型结构，具有非常多的自由度，响应的计算耗费是巨大的。一般的计算过程是这样的：
求该系统的特征值与特征向量
由该式的特征方程：det（-W2[M]-[K]）=0
求得N个特征值及相应的特征向量
，
，…，
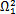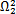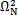
于是qr可以单独求解。
在求得所有的qr后，即求得{q}后，可按下式来计算结构系统各点的响应
{x}=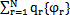 
上述过程称为模态叠加法， qr可以理解为第r阶固有振动模态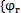
对实际振动{x}所作的贡献。各阶模态所作贡献的大小除取决于结构本身的特点外，还取决于结构受激励力的频率范围，以及激励力分布的情况。理论上，对于一个N自由度的系统，可以通过方程解耦确定模态坐标响应，然后通过线性变换得到物理坐标响应。但实际上在一个系统的振动中仅是较少几个模态在起主导作用，因此只考虑这些模态的作用，而无需求解全部的方程，这样做虽然是近似的但却有足够满意的精度，这便是模态叠加法的出发点。
6.4.4 模态综合
由于对我们起指导作用的是一个系统的动特性，即系统的固有频率和振型，因此，在求得单个构件的固有频率和振型后，我们应进行模态综合，即部件的模态分析或称动特性分析。
在模态综合中应请注意如下几点：
在求得自由系统的模态后，若要再考虑边界条件的影响，是可以通过计算来完成的。反之，在某种非自由边界条件下取得的结果，很难被转化到其它的边界条件的情况。故单个构件的模态应是自由边界下得到的。
特别应该指出的是，自由系统的模态中，不应忽略刚体模态。仅有部件弹性模态不能用于整体结构的综合。
部件是整体结构的一部分。部件的模态向量应保证其在与整体连接的那些点有值。否则不能进行整体模态综合。
部件的分析模态的阶数一般少于部件的自由度。但一定要大于部件在整体连接时的连接点自由度数。
6.4.4.1 模态综合理论：
这里所述的仅是模态综合理论中的一种方法，在这种方法中，采用各部件的自由模态（或非约束模态）来进行综合，但综合后的整体结构模态数，将由各部件所包含的模态数来确定。
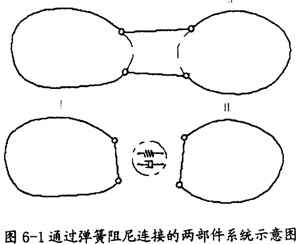
设有部件I和部件Ⅱ，通过弹簧和阻尼构件相连接，如图6-1所示。对于部件I，应用
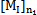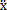{}+[KI]{xI}+[CI]{
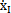}={fI} （6-1）
式中{fI}仅为作用于连接点上的内力。假定我们已对部件I作了模态分析，因此上式可转化为用模态坐标表达的形式
将（6-6）式代入（6-5）式，得
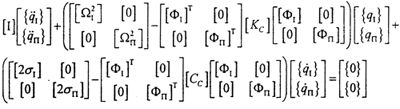
由于[KC]和[CC]不是对角阵，因此上式是一组耦合方程。上式缩写为
[I]{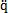
}+[KCO]{q}+[CC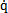O]{
}={O}
对于小阻尼系统，可按常规方法，先用
[I]{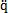}+[KCO]{q}={O}
求组合系统的特征值及特征向量，然后可建立组合系统的模态模型。（不难看出，此处组合结构整体的特征值的数目由各部件的模态数来确定，而不是由它们的结构几何坐标数确定的）
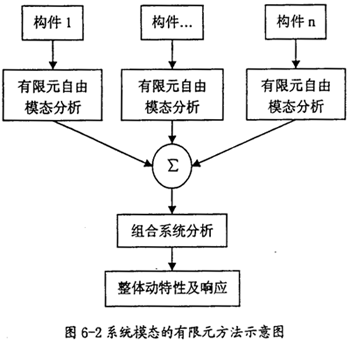
6.4.5 系统模态的有限元方法
通过对系统中的各构件进行有限元自由模态分析，得到各构件的自由模态（当然也包含了6个刚体模态），以各构件的连接关系为依据，建立边界条件，然后进行模态综合，即可计算得到整个系统的动特性和响应。其过程如图6-2。
上一页
下一页
