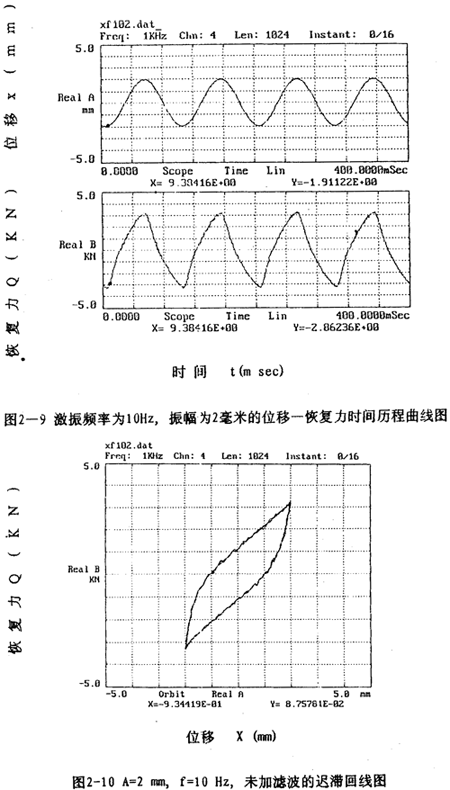
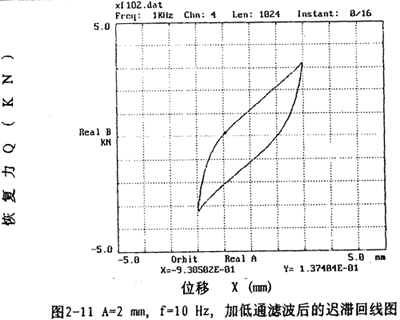
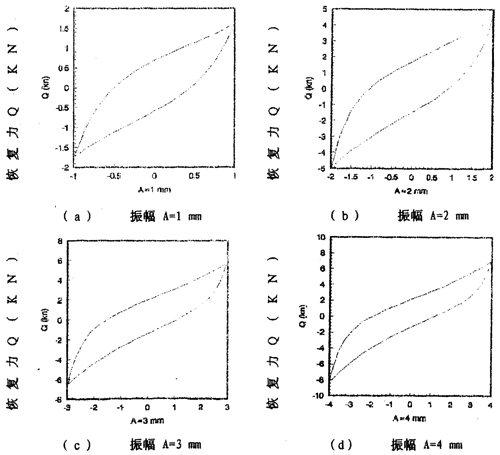
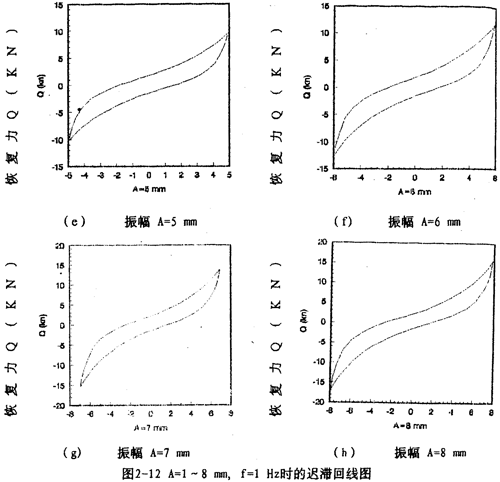
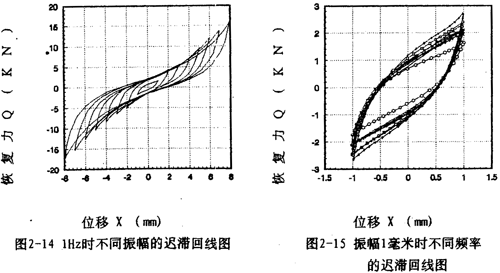
图2-9(见26页)表示激振频率为1OHz,振动位移幅值为±2毫米的位移和恢复力时间历程图,图2-10(见26页)、图2-11(见27页)为对应的迟滞回线图。图2-l2(见27、28页)表示激振频率为IHz,振动位移幅值分别为±(1-8)毫米的位移一恢复力图,图2-14(见29页)则为图2-12的合图,由图2-14同频率不同振幅的八条迟滞回线分析可知,大挠度刚丝绳弹性联轴器的动刚度与振动幅值有关,同时,从迟滞回线面积(表示联轴器阻尼所耗散的能量)可知联轴器的阻尼与振动幅值也有关,即联轴器的动刚度和阻尼均是振幅的非线性函数。
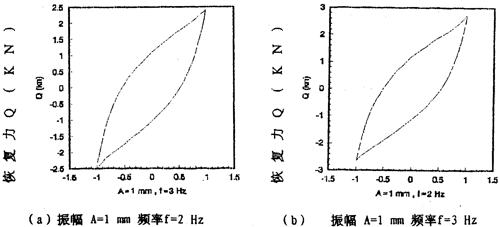
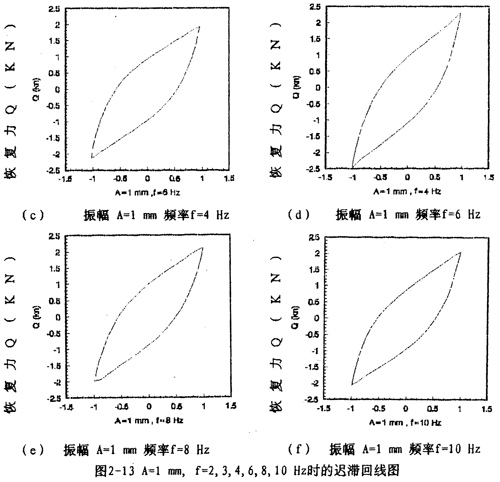
图2-13(见28、29页)表示振幅为l毫米,激振频率分别为2,3,4,6,8,10Hz的迟滞回线图,图2-15(见29页)表示振幅为1毫米,激振频率为1,2,3,4,6,8,10,20,30Hz的迟滞回线合图。由图2-15可知,弹性联轴器的动刚度与振动频率有关,即随着频率增大,对应的迟滞回线的恢复力与位移的比值变小,当频率在8Hz至30Hz范围内时,迟滞回线基本重合,由此可知钢丝绳联轴器动刚度在一定频率范围内与频率有关、当频率增大到8Hz以后,联轴器的动刚度不再随频率变化而变化,因而联轴器的动刚度在一定频率范围内与频率有关,当频率增大到8Hz以后,联轴器的动刚度不再随频率变化而变化,因而联轴器的动刚度在一定频率范围内是频率的非线性函数,当频率增大到一定值后,动刚度与频率无关,同样,联轴器的阻尼在一定频率范围内的频率的非线性函数,当频率增大到一定值后(这里是8Hz),阻尼与频率无关。
2-5 小结
通过对钢丝绳弹性联轴器的振动试验、信号处理和分析,可以得到以下结论:
1.开发MTS材料试验机对大挠度弹性联轴器进行大位移振动试验是可行的,解决了激振器或振动台不能同时满足大位移、频率和激振力达到一定要求的难题,为大位移振动试验开辟了新的途径。
2.钢丝绳弹性联轴器能产生动态大位移,具有补偿主机在运行中出现大位移的能力。联轴器及钢丝绳弹性元件能在设计范围内正常工作,但有的弹性元件出现钢丝断丝现象,夹持板在低频大位移振动时变形较大,因此有必要对弹性元件的联接方式进行改进。
3.钢丝绳弹性联轴器的恢复力具有非线性迟滞特性,在大位移振动情况下表现出动刚度非线性和阻尼非线性的特性,联轴器的动刚度是振动幅值和频率的非线性函数,但当频率增大到一定值后,动刚度仅为振幅的非线性函数。同样,联轴器的阻尼在一定频率范围内是振幅和频率的非线性函数,但当频率增大至一定值后,阻尼仅是振幅的非线性函数。因此大挠度弹性联轴器的本构关系是一非线性泛函。
4.以上研究成果为联轴器恢复力数学模型的建立、参数辨识提供了依据和准备了数据。
上一页
下一页







