第三章 具有非线性迟滞特性钢丝绳联轴器建模与参数辨识
3-1 引言
由上章对联轴器振动试验研究结果可知，在大位移振动情况下，联轴器表现出非线性迟滞特性．这一特性直接与联轴器动刚度及阻尼有关，当这种联轴器用于船舶推进轴系时，将影响到轴系的动力特性，因此弄清楚联轴器恢复力与动刚度和阻尼的关系，即建立联轴器恢复力的数学模型是十分重要的，对于深人分析研究推进轴系的动力特性也是不可缺少的。
由钢丝绳联轴器的
-x迟滞回线可知，联轴器的迟滞特性不宜用双线性模型来描述，主要原因是双线性模型与联轴器的动态迟滞回线外形相差甚远，双线性模型将系统刚度系数处理成二个线性刚度系数。这不足以描述钢丝绳联轴器的非线性迟滞特性中的非线性刚度系数，双线性模型阻尼仅处理为干摩擦阻尼，也不足以描述联轴器阻尼的复杂成分。一阶微分方程模型主要用于迟滞系统的随机响应分析中，这种模型用于计算迟滞系统的稳态动力响应很不方便，模型中各参数的物理意义不明确，模型形式不利于各参数的辨识，而且弹性力和阻尼力在恢复力表达式中不显现，不利于理论分析。基于平均和等效原理的迹法和以此为基础K0等建立的模型都有自己的不足，前者只能描述迟滞恢复力与位移和速度的关系，而不能全面描述迟滞恢复力与各振动参数的关系，后者只能描述三个阶次非线性弹簧刚度，其应用范围受到限制。由此可知，现有描述迟滞特性的数学模型都不能用来描述联轴器的非线性迟滞特性。因此，本章将在前人研究的基础上，研究联轴器动刚度和阻尼的特性，建立既能合理描述联轴器非线性迟滞特性又能满足较高精度要求的数学模型。
3-2 拟合分解恢复力-位移迟滞回线
上一章的试验研究表明，钢丝绳弹性联轴器的本构关系十分复杂，其恢复力是联轴器动刚度和阻尼的函数，而动刚度和阻尼又是振幅和频率的函数。因此，我们将依靠试验获得的测量数据，在迹法和文献的基础上，深人研究联轴器迟滞特性，建立联轴器的数学模型。
由前面联轴器位移-恢复力试验可知，迟滞回线可以分为上、下两条，分别对应于速度大于零和速度小于零。在钢丝绳弹性元件性质相同和安装几何对称的情况下，上、下两条恢复力曲线可以认为是位移反对称的。于是可以用幂函数多项式，按最小二乘法原理来拟合代表试验数据的上、下两条恢复力曲线，设用于拟合上迟滞回线数据的幂函数多项式为：
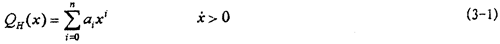
根据反对称，用于拟合下迟滞回线数据的幂函数多项式为：
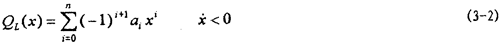
式中，H，L分别为联轴器迟滞恢复力上、下曲线，x为位称，ai为幂函数多项式系数。
幂函数多项式所取项数n按拟合的迟滞回线形状和对表达式要求的精度而定。将（3-1）和（3-2）式中幂函数多项式的奇、偶次项分开写，可进一步表示为：
经以上数学处理，联轴器的动态迟滞回线可以分解成1（x）和2（x，
）两部分，即联轴器的迟滞恢复力由两部分组成。式中n取奇数。从几何意义上讲，第一部分为一条单值非线性函数曲线，第二部分为一条双值的非线性闭合曲线。从物理意义上讲，第一部分代表迟滞恢复力中的非迟滞非线性弹性恢复力；第二部分代表迟滞恢复力中的纯迟滞非线性阻尼力。
由试验知，联轴器的迟滞恢复力不仅是位移x和速度的函数，而且还是振幅A和频率ω的函数，因此迟滞恢复力的数学模型设为：
（x，
，A，ω）=1（x，A，ω）+2（x，A，，ω） （3-7）
由此可见，迟滞恢复力的函数关系相当复杂，
由试验还可以知道，频率增大至一定值后动刚度和阻尼仅是振幅A的非线性函数，在这种情况下，迟滞恢复力的数学模型可表示为：
（x，，A）=1（x，A）+2（x，A，） （3-8）
由此，我们得到两种形式的联轴器恢复力数学模型，前者为考虑频率影响的数学模型，后者为不考虑频率影响的数学模型。
至此，尽管我们将迟滞恢复力拟合分解成了两部分，但是l和2取什么样的函数形式，仍然是一个难题。对此，分三步来研究。第一步先求出不同频率和振幅下迟滞数据回线的拟合迟滞回线，得到对应的各阶离散的刚度系数值，以及迟滞阻尼耗能值；第二步再找出这些数值与频率、振幅的函数关系表达式，从而得到l和2的函数关系表达式，第三步，通过参数辨识，寻找出l和2表达式中的各参数。
由迟滞回线的形状可知，联轴器具有强非线性的特性，为了在数学模型中反映出强非线性的特性，选9阶幂函数多项式来拟合上、下迟滞回线（n=9)，对一定频率和振幅的每一组试验迟滞回线数据，由线性最小二乘法原理一辨识对应的各阶拟合系数。对图2-14中各迟滞回线数据进行拟合，将所得的拟合迟滞回线与图2-14的迟滞回线画在一起，如图3-1（a）所示，由此图可知，两者重合性很好。
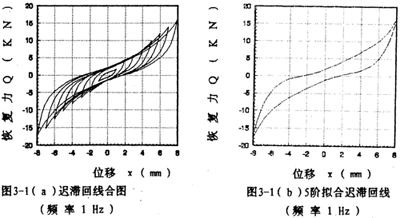
为了说明5阶和7阶幂函数多项式拟合的精度情况，以振幅A=8毫米，频率为1赫兹为例，画出拟合回线分别如图3-1（b）、3-1（c）所示，将它们与对应试验回线图3-1（d）比较，可知7阶拟合精度高于5阶。图3-1（e）为图3-1（b）与图3-1（d）的合图。
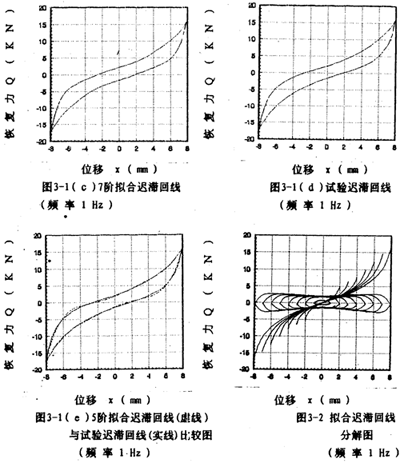
为了得到（3-6）式所示的l，2，将拟合得到的各幂函数多项式奇、偶次项分开写成（3-5）式形式并作对应的曲线图，如图3-2（见34页）所示，这样就将恢复力分解成了单值非线性函数曲线和双值的非线性函数闭合曲线，由此得到了对应的l（x）和2（x，）的若干组函数表达式：
式（3-9）中各系数a2i-1实质上代表联轴器弹性恢复力在对应频率、振幅下的各阶刚度系数。
3-3 联轴器数学建模
一、不考虑频率影响的数学模型
由于联轴器恢复力仅在一个小范围内受频率的影响，当频率达到一定值后，联轴器恢复力仅是振幅的函数，在这种情况下，数学模型的表达式为（3-8）式。下面分别研究l和2函数表达式的结构形式。
1.非迟滞非线性弹性恢复力l的数学模型
在不考虑频率影响的情况下，联轴器弹性恢复力，由以上分析，可以建立其数学模型如下：
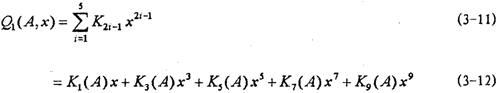
式中K1（A）--K9（A）是钢丝绳联轴器第一～九阶弹簧刚度函数。
这样的数学模型充分地考虑了高阶非线性弹性力的影响。式中K2i-1（A）仅是振幅的函数，其数学模型为：
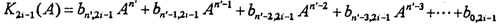（i=1，2，3，4，5） （3-13）
式中n′根据精度要求而定。
2.迟滞非线性阻尼力2的数学模型
由拟合迟滞回线分解图3-2中各闭合曲线知，联轴器中的阻尼成分非常复杂，有可能是多种阻尼的组合，根据联轴器弹性元件变形及工作情况，可以认为联轴器阻尼含有粘性阻尼和干摩擦阻尼的成份较多，因此，在这种情况下我们建立以下二种阻尼力模型：
(1）复合型阻尼力模型
2=a[a0+a2x2+a4x4+a6x6]sgn（）+C||nsgn（） （3-14）
式中第一项代表除粘性阻尼力和干摩擦力以外的其它阻尼力成份，系数α决定这些阻尼力所占比例，故定义为阻尼比例控制系数；第二项代表粘性阻尼力和干摩擦阻尼力综合阻尼力成份，当n=o时，这项为Csgn（），代表干摩擦阻尼力，当n=1时，这项为C||sgn（），代表粘性阻尼力，当n在（0，1）区间变化时，第二项代表的是粘性阻尼力和干摩擦阻尼力的混合阻尼力，系数n决定两种阻尼各占份额多少，定义为粘摩阻尼分配系数。式中a0,a2，a4，a6，C,n和α均是振幅的函数。
(2）等效粘性阻尼力模型
用等效粘性阻尼来描述迟滞非线性阻尼，其恢复力构建为：
2=C（A，ω） （3-15）
由于联轴器阻尼成份的复杂性，以上建立的二种阻尼恢复力模型中哪一种用来描述联轴器阻尼力更为合理，有待于参数辨识后才能确定。对于模型（3-14)，我们将先辨识出在不同振幅下模型中的各个参数，然后再找出这些参数与振幅的函数关系。对于模型（3-15)，我们将根据一个振动周期内迟滞非线性阻尼所耗散的能量与等效粘性阻尼所消耗的能量相等的能量关系找出等效粘性阻尼函数C(A，ω）与振幅和频率的关系。
上一页
下一页
