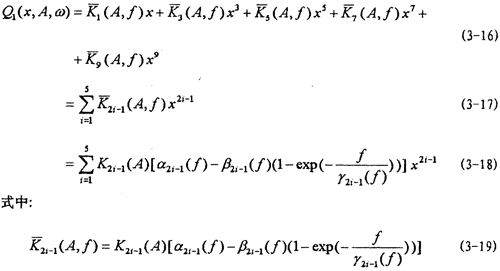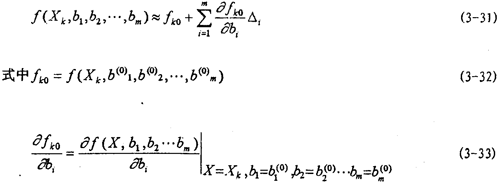二、考虑频率影响的数学模型

在这种情况下，联轴器的数学模型的表达式为（3-7）式，下面分别讨论_l和₂函数表达式的结构形式：

1.非迟滞非线性弹性恢复力_l的数学模型

由试验研究知道，联轴器的弹性恢复力不仅是振幅的的函数而且还是频率的函数，随着频率的增大，在一定频率范围内，弹性恢复力逐渐减小，然后趋于一定值，根据这一特性，在建造弹性恢复力新的数学模型时，引进一个能描述这一特性的指数函数项e^-flr（f），这样，新构建的弹性恢复力数学模型为：

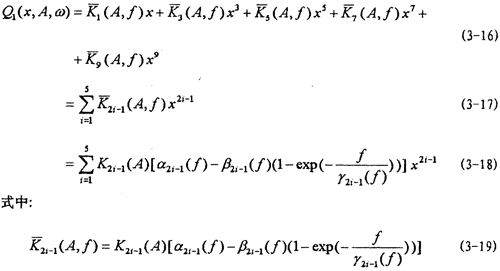
同时，定义几个新函数参数，a_2i-1（f）为刚度幅值频率影响系数，它表示联轴器弹性元件各阶刚度的幅值受频率变化影响的程度；β_2i-1（f）称为刚度幅值频率衰减系数，表示弹性元件各阶刚度的幅值随频率增加的衰减程度；y_2i-1（f）称为刚度频率衰减系数，表示弹性元件各阶刚度随频率增加的衰减速率，y_2i-1（f）愈大，刚度值随频率减小的速度就愈慢，反之，则愈快。从理论上讲，只有当f值趋于无穷大时，exp{-f/[ y_2i-1（f）]}才趋于零，各阶刚度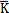_2i-1（A，f）才趋于各自的定值K_2i-1（A）[α_2i-1（f）-β_2i-1（f）]。但事实上，由于指数曲线开始变化较大，而后逐渐缓慢，所以，实际上f达到一定值后，exp{-f/[ γ_2i-1（f）]}已经很小了，例如，设f=5 γ_2i-1（f），这时有：

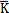_2i-1（A，f）= K_2i-1（A）[α_2i-1（f）-β_2i-1（f）（1-e^-5）]

                           = K_2i-1（A）[α_2i-1（f）-β_2i-1（f）×0.99326]               （3-20）

当频率f=8，10，…，30赫兹时，刚度不再随频率的变化而变化，由此可得γ_2i-1（f）=1，6,2，…，6；α_2i-1（f）-β_2i-1（f）×0.99326=β_c，这些参数值和关系式在辨识（3-19）式中参数时，可作为已知条件应用。

从以上分析可知，(3-18）式表示的数学模型能客观地反映联轴器弹性恢复力随振幅和频率变化的规律。

2.迟滞非线性阻尼力₂的数学模型

当同时考虑振幅和频率对迟滞阻尼力₂的影响时，₂将是振幅和频率的函数，如果经过参数辨识说明（3-14）形式的数学模型能合理地描述阻尼力，那么，在同时计及振幅和频率对迟滞阻尼力₂的影响时，我们仍建立迟滞阻尼力的数学模型表达式为（3-14）式的形式，不过其中各系数不仅是振幅A的函数而且还是频率f的函数，建立的第二种数学模型仍以等效粘性阻尼来描述迟滞非线性阻尼，与(3-15）式所不同的是，在此建立联轴器阻尼耗能的函数时，同时考虑联轴器迟滞回线面积随振幅A和频率f变化的规律，而在建立（3-15）式时仅考虑联轴器迟滞回线面积随振幅A的变化规律。为了叙述方便，这些问题在参数辨识一节中讨论。这样，这二种阻尼力模型为：

综上所述，将（3-12）式与（3-18）式比较，将（3-14）～（3-15）式与（3-21）～（3-22）对应式比较可知，后者同时考虑了振幅A和频率f对联轴器恢复力的影响，因而适用范围较前者仅考虑振幅A的影响时更大，但后都数学表达式复杂，大大地增加了参数的辨识难度。由试验研究知，频率变化对恢复力影响范围较小，为了简化计算用（3-12）和（3-14）～（3-15）较好。

3-4  联轴器数学模型参数辨识

本节将利用试验数据，根据上节建立的联轴器恢复力数学模型的类型，联分别选用线性参数辨识方法和非线性参数辨识方法，按最小二乘法原理，辨识联轴器数学模型中的参数，找出各参数与振幅和频率的关系，得到联轴器恢复力由弹性和阻尼力描述的函数关系式。

一、参数辨识的难点

联轴器数学模型函数关系的复杂性以及函数关系式中参数的非线性都给参数辨识工作带来困难。针对这些情况，对数学模型中某些参数随振幅和频率变化规律还不能给出表达式时，我们先求出这些模型在不同振幅和频率下，各参数随振幅和频率变化的离散值，然后根据这些离散值随振幅和频率变化的规律，来定出函数表达式，在此基础上再进一步找出这些参数与振幅和频率的函数关系，最后得到联轴器恢复力与振幅、频率、位移和速度的表达式。

二、参数辨识

1.辨识不考虑频率影响数学模型的参数

不考虑频率影响时联轴器的数学模型为（3-12）～（3-15）式，

a.非线性弹性恢复力_l数学模型中参数的辨识

此中情况下，_l的表达式为（3-12）和（3-13）式。由这两式可知，模型中含有九阶的高次非线性弹性力，其各阶动刚度K_2i-1 (A）是振幅的函数，数学模型为一个n′阶的幂函数多项式，K_2i-1 (A）是各参数b_0，2i-1～b_n，2i-1 (i=1,2，…，5）的线性函数。于是各阶动刚度K_2i-1 (A）中各参数辨识可归结以下最小二乘法问题：

已知K_2i-1 (A）是关于自变量X=[A，A²，…A^n′]^T和待定参数B=[ b_0，2i-1，b_1，2i-1，…，b_n′，2i-1]^T的形式已知的函数（3-13)，简写成：

K_2i-1 (A）=f（X，B）                            （3-23）

今给出（X，K_2i-1 ）的n对试验值：

（X_K，K_2i-1，K）      （k=1，2，…，n）              （3-24）

要求确定参数B使

得一组线性方程组，在n>k的情况下，联立求解这一线性方程组即可求得唯一的一组B值。根据此法求得（3-13）式中参数值并代回可得：

将（3-27）式中刚度函数作成曲线如图3-3(a）-（e）所示，由一阶动刚度函数图3-3(a）可知，振幅在lmm～2mm范围内时，动刚度随振幅增大而增大，呈硬特性；当振幅在2mm～7mm范围内时，动刚度随振幅增大而减小，呈软特性；当振幅在7mm～8mm范围时，动刚度随振幅增大略有回升。由此图可知，在联轴器初始小振幅和极限振幅附近范围内，动刚度呈硬特性，而在中间振幅范围内呈软特性。K₅（A）和K₉（A）也具有类似的特性。而K₃（A）和K₇（A）在小振幅时呈软特性，这样的动刚度特性满足船舶缓冲减振降噪的要求，即在一般低能量风浪流作用下，该联轴器钢丝绳元件的变形小，动刚度大，呈硬特性，这能保证船舶推进轴系的基频高于风浪流的显著能量频率；在大能量风浪流和冲击作用下时，联轴器由于载荷增大而变形增大，这种情况下动刚度软化，使船舶推进轴系频率变小，向远离大能量风浪流和冲击显著能量频率一侧偏移，在迟滞阻尼下耗散能量，使轴系冲击振动响应降低。由（3-27）式和（3-12）式可作出相应的弹性恢复力单值曲线如图3-4所示。将图3-4中代表弹性恢复力的单值曲线与图3-2中的单值曲线比较可知，(3-12）式能较好地描述联轴器弹性恢复力随振幅变化的规律。

b.非线性阻尼力数学模型中参数的辨识

此情况下，建立了二种数学模型（3-14）式和（3-15）式。对于（3-14）式描述的模型，₂是参数n的非线性函数，因此，在进行参数辨识时，需要用非线性参数的辨识方法。此时，这种模型中各参数的辨识可归结为如下的最小二乘法问题：

已知₂是关于自变量X=[x₁，x₂，…，x_p]^T和待定参数B=[b₁，b₂，…，b_m]^T的形式已知函数（3-14）式，简写成：

₂=f（X，B）                   （3-28）

对于给定的n组试验数据值（X_k，_2k），要求确定参数B使

为最小。对于这种非线性参数识别，很难直接进行求解，通常采用逐次逼近的方法处理，在此采用高斯-牛顿法来辨识。高斯-牛顿法的基本思想是：先给出各参数b_i的一个初始值，记为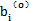，初值与真值之差为△_i，即有：

b_i=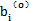+△_i             （i=1，2，…，m）                    （3-30）

这样，确定b_i的问题就变成了确定△_i的问题。为确定b_i，在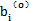邻域内将函数f（X，B）作代台劳级数展开，并略去△_i的二次及二次以上项得：

上一页

下一页