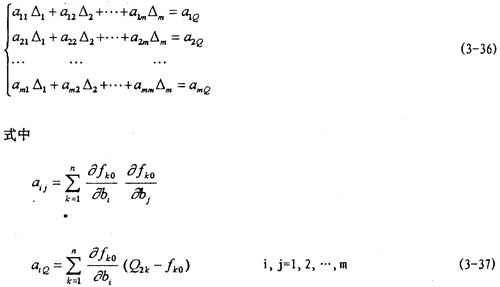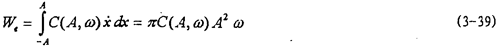当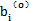
给定时，fko和
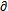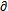fko/bi都是自变量X的函数，可直接算出，将（3-31）式代入（3-29）得：
由多元函数极值存在的必要条件：
得以△i为未知量的一组m个联立方程组
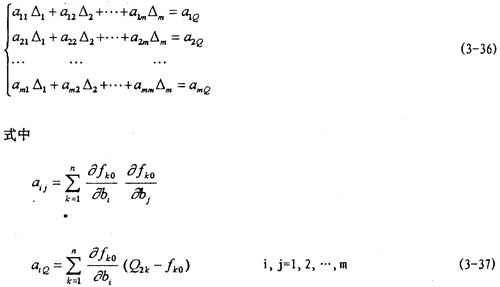
当试验数据值（Xk，
2k），（k=1，2，…，n）和初始近似值bi(0)(i=1,2,...,m)给定后，系数aij及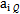
均可算出，因此由方程组可解出△i，进而得bi的值。当算出的|△t |值较大的时，可令当前的bi值代替原来的初始近似值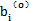，重复计算aij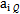，，并解方程组（3-36）得新的△i，进而得bi。这种过程可以重复进行，直至|△t |的值小到给定的精度为止。
对于非线性参数辨识问题，并在不于迭代工作量有多大，而是在迭代逼近过程中是否收敛，即迭代过程有可能不按上述方式完成，出现计算溢出，方程组系数矩阵病态等毛病．出现这些问题的原因大致有三种：一是逼近试验数据点（Xk，2k）的数学模型假设与数据点甚远，在这种情况下，必然重新分析系统的内在机理，建立符合系统特性的新数学模型；另一种是初值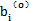选得不好，台劳级数展开式完全失真，迭代得到的新bi有可能比原来的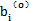更远离真解，且越迭代越糟糕，最后发散，在这种情况下，迭代是否收敛，关键在于初值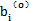的选择；第三种是参数辨识的算法不适合或对初值选取的要求太高，在这种情况下，需选择更合适的算法或选择对初值选取要求较低的算法。
按照以上算法，编制了计算机软件对（3-14）模型中的参数进行了辨识，结果讨论如下：
对（3-14）模型，用不同振幅下联轴器试验数据中代表阻尼力的数据来进行参数辨识，辨识结果是迭代计算不收敛，分析其原因，我们认为，一是因为需辨识的参数较多，初始值不易选得与真值较接近，致使迭代不成功；二是此算法可能不适合此模型的参数辨识。因此，有待于寻找能辨识数学模型表达式中参数的新的有效辨识方法。
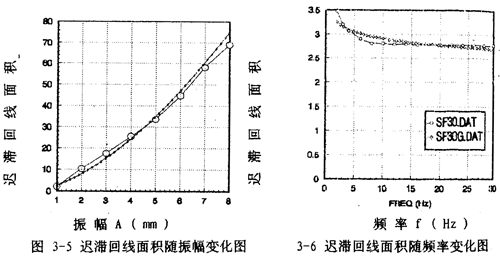
第二种模型是（3-15）式，在这种情况下，用阻尼耗能的能量关系来辨识阻尼力与振幅等参数的关系。由图3-1可知，联轴器每振动一周所消耗的能量，即迟滞回线的面积S是振幅A的函数。由数值积分，可以算出各振幅变化时迟滞回线面积，由此可得迟滞回线面积与振幅的一一对应关系，将这些一一对应的数据点画成图，如图3-5中大圆点曲线所示，由此分析迟滞回线面积随振幅变化的规律，可建立其函数关系为：
Sga（A）=asAbs （3-38）
式中as和bs为待辨识参数。由（3-38）可知，面积是参数bs的非线性函数，参数辨识时用非线性参数辨识方法，高斯-牛顿法，辨识结果为as=2.56969，bs=1.62309，代回（3-38）式并画出曲线如图3-5中小点曲线所示。由此可以看出，(3-38）式能较好地描述迟滞回线面积（即联轴器阻尼耗能）随振幅变化的规律．在用等效粘性阻尼来代替迟滞非线性阻尼的情况下，在具有相同振幅的正弦振动时，每周由等效粘性阻尼力耗散的能量为：
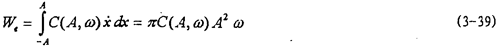
因为Sga=We，由（3-38）与（3-39）可得联轴器阻尼函数C（A，ω）：
将（3-40）式代入（3-15）式得联轴器阻尼力模型：
值得注意的是此阻尼力模型的参数辨识是在研究阻尼耗能过程中，仅考虑振幅对耗能的影响下得出的，而没有考虑频率对耗能的影响，式中频率项的出现是由于用等效粘性阻尼代替迟滞非线性阻尼所致。将（3-41）式画成曲线得图3-4中各椭圆，与图3-2中的闭合曲线相比较可知（3-41）式较好地描述了迟滞非线性阻尼力。将（3-11）、（3-27）和（3-41）式代人（3-8）式即，得联轴器恢复力数学模型的函数表达式。
2.辨识考虑频率影响数学模型的参数
考虑频率影响时联轴器的数学模型为（3-17）-（3-22）式。
a.非线性弹性恢复力Ql数学模型中参数的辨识
此情况下，1的表达式为（3-18）-（3-19）式，由于数学模型中参数辨识的复杂性以及待辨识参数的非线性性，在辨识过程中，先辨识出在不同振幅和频率下模型中的各参数α2i-1，β2i-1和γ2i-1，然后根据这些参数离散散值随频率变化的规律，建立它们与频率之间的函数关系，再辨识这些函数关系式中的各参数，从而得到α2i-1 (f)，β2i-1（f）和γ2i-1 (f）的函数表达式，最后得到动刚度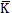
2i-1（A，f）随频率和振幅变化的数学模型和弹性恢复力教学模型。
我们用高斯-牛顿法的最小二乘法来辨识，辨识结果是迭代计算不收敛，分析原因认为：迭代计算不收敛，一是初值选择不合理，二是此算法对初值要求太高。尽管如此，但根据对联轴器非线性弹性恢复力随频率变化的规律分析，我们仍认为用（3-18）式来描述联轴器弹性恢复力l=（x,A，ω）是客观的和合理的，式中未知参数的辨识有待于寻找新的有效的辨识算法。
b.非线性阻尼力2数学模型中参数的辨识
此情况下，建立的数学模型为（3-21）-（3-22）式。对（3-21）式，辨识所用方法和试验数据与辨识（3-14）式相同，所得结果是迭代计算不收敛，究其原因, 认为是所用辨识算法不适合此模型的参数辨识，同时此算法对初值的要求比较高。
为了解决以上未决的参数辨识问题，我们又用了一种算法，Marquardt算法对（3-14）、（3-18）和（3-21）模型进行了参数辨识，迭代计算仍不收敛。为了解决这一问题有待进一步寻找有效的辨识算法。
对于（3-22)模型，我们用阻尼耗能的能量关系来辨识阻尼力与振幅和频率的关系。在前面，迟滞回线面积（即阻尼耗能）与振幅的函数关系已建立起来，见（3-38）式，而且式中参数也已辨识出。同样，用数值积分，可以算出振幅一定，频率变化时迟滞回线的面积，由此得出迟滞回线面积与频率的对应关系，将这些对应关系画成曲线如图3-6中大圆点曲线所示。由迟滞回线面积随频率变化的规律分析，可建立其函数关系为：
Sgf（f）=affbf （3-42）
式中af和bf为待辨识参数。由此式知，面积是参数bf的非线性函数，用高斯-牛顿法辨识得af=3.40234,bf=-0.0684433，代回（3-42）式并画曲线如图3-6中小点曲线所示。由此可知，(3-42）式能较好地描述迟滞回线面积随频率变化的规律，阻尼耗散的能量随频率的增大而减小。综合考虑（3-38）和（3-42）式中阻尼耗散的能量随振幅和频率变化的规律可知，阻尼耗能随振幅的增大而增大，随频率的增大而减小，由此可建立联轴器阻尼耗能（即迟滞回线面积）随振幅A、频率f变化的数学模型如下：
式中ag,p,q为待定参数。由此式可知，联轴器阻尼耗能是振幅和频率的非线性函数,也是参数p,q的非线性函数。在辨识时，采用高斯-牛顿法。根据（3-38）、(3-42）两式及其参数，可知（3-43）中αg参数的变化域在（2.56969,3.40234）内，q值在1.62309附近，而p值大约在0.068443附近，据此分析，三个参数的初值分别选为：
=3.0，q(0)=1.0，p（0)＝0.1
将这三个初值输人程序进行运算，一次计算成功，三个参数值为：
αg=3.382818，q=1.451636，p=0.06649397 (3-44)
将这些参数代人（3-43）式即得联轴器阻尼耗能随振幅和频率变化的函数关系式。
根据等效原理（3-34）式和Sg=We以及（3-44) 式可得等效粘性阻尼函数为：
将（3-44）、（3-45）式代入（3-22）式得阻尼力数学模型为
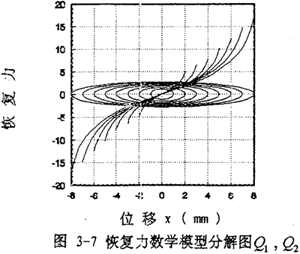
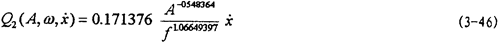
作出（3-46）式的曲线图如图3-7中椭圆所示，将图3-7中椭圆与图3-4中对应椭圆相比较可知，式（3-46）能较好地描述非线性迟滞阻尼力。
3-5 关于联轴器建模与参数辨识的进一步研究
一、数学建模与参数辨识
在对前面关于联轴器建模与参数辨识工作进行思考和对联轴器试验结果进行进一步深人分析后，提出联轴器恢复力数学模型新表达式：
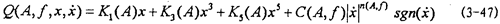
即恢复力(A,f,x，
）是振幅A、激励频率f、瞬态位移x和瞬态速度的函数，或者说恢复力Q是刚度函数K1（A），K3（A），K5（A）和阻尼函数C(A,f）以及阻尼成分函数n(A,f）的函数，其中阻尼成分函数n(A,f）描述阻尼的组成情况，n（A,f）=0时，阻尼为干摩擦阻尼，n(A,f)=1时，为粘性阻尼，0＜n（A,f)<1时，阻尼由粘性阻尼和干摩擦阻尼组成，n（A,f)>1时，阻尼成为“高阶”阻尼。对于（3-47)式，当振幅与频率一定时，式中的Kl（A），K3（A)，K5（A）和n（A,f）均为定数，当振幅A和频率变化时，它们均是函数，因此参数辨识实质上是参数函数的辨识。首先我们用非线性参数辨识方法Marquardt法，根据试验所得的数据，按照（3-47）式对每一迟滞回线进行参数辨识，可以得到对应的K1（A)，K3（A），K5（A),C(A,f)和n（A,f）值，对每种工况下的数据随振幅和频率变化趋势进行分析后，可以建立刚度函数、阻尼函数和阻尼成份函数的数学表达式为：
上一页
下一页
