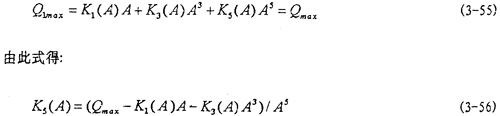然后用线性参数辨识法和非线性参数辨识法，根据上面已经得到的各个工况下K1（A)，K3（A），K5（A),C(A,f)和n（A,f）的数值对（3-48）、（3-49）、（3-50）式中各参数进行辨识，将辨识得到各参数代入（3-48）、（3-49）和（3-50）式得：
关于K5（A)的辨识采用以下方法：
当位移x达到最大值A时，联轴器恢复力Q达到最大值，弹性恢复力也达最大值，此时有：
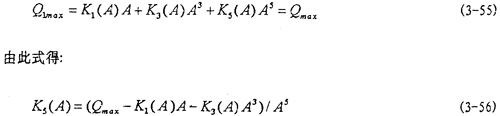
式中K1（A)，K3（A）已求得。由试验迟滞回线恢复力最大值与振幅的数据，可辨识出（3-56）式的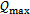
为：
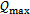（A）=-5.16965×10-5A7+2.21538×10-5A6+0.0241174A5-0.375207A4+2.55596A3-8.88624A2+16.8085A-
8.37136 （3-57）
将（3-51)、(3-52）和（3-57）式代人（3-56）即求得K5（A)。至此，(3-47）式中的各参数函数已全部辨识出。将这些参数代入(3-47）式就得到联轴器恢复力数学模型。
二、结果分析与比较
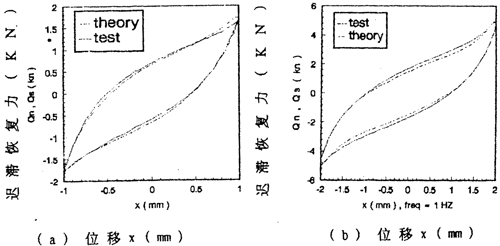
由数学模型（3-47) 计算可以得到不同激励频率和振幅下联轴器恢复力迟滞回线数据，为了证实（3-47）的正确性，下面画出频率为1赫兹、振幅为1～8毫米各工况下数学模型计算的理论数据和试验数据表示的迟滞回线图，如图(3-8)(a）～（h)（见51～52页）所示，图中虚线为理论回线，实线为试验迟滞回线。从图中可知，理论迟滞回线十分接近试验迟滞回线，由此可以说明建立的联轴器数学模型（3-47）式可较好地描述恢复力随振幅A频率f、瞬时位移x和速度
变化的规律，较圆满地解决了联轴器恢复力建模与参数函数辨识的难题。
为了进一步分析联轴器的阻尼特性并与用拟合分析解法和阻尼等效原理建立的数学模型（3-12）、（3-13）、（3-14）作比较，画出由数学模型（3-47）式分别描述的弹生恢复力
1和阻尼力>2的曲线图，如图（3-9）a）～（h）所示，图中单值曲线为弹性恢复力1。双值闭合曲线为阻尼力2。
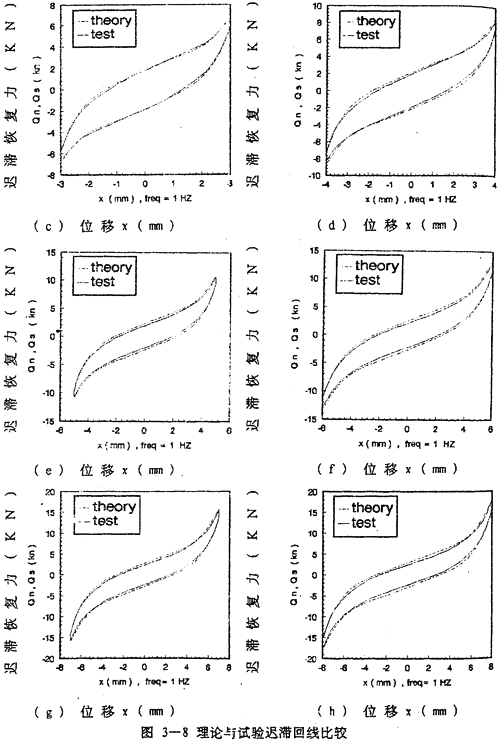
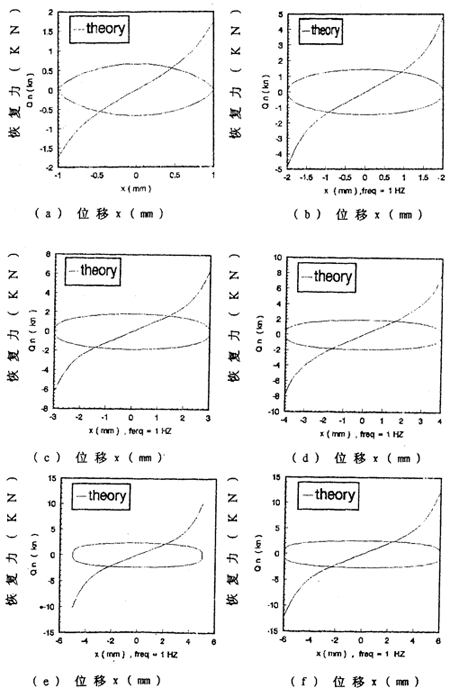
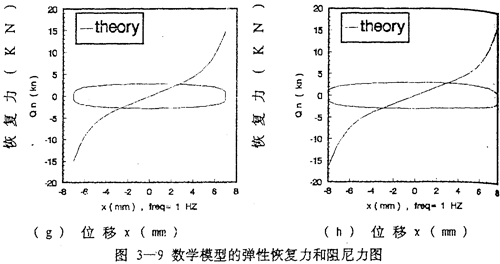
(1).从图3-9(a）-（h）中可以看到：双值闭合曲线的形状随振幅的增大，从橄榄形变成椭圆形，再变成棒槌形。说明联轴器的阻尼成分不是单一的，而是多种阻尼的组合，这些阻尼在不同的振幅下出现的大小比例不同，振幅为1毫米时，见图3-9(a）图，“高次”阻尼成分较多，而干摩擦阻尼和粘性阻尼成分较少，这时阻尼力闭合曲线的形状呈橄榄形，这是因为振幅较小时，联轴器弹性元件中的钢丝绳股与股之间所受的力和位移都较小，还没有产生相对滑移。随着弹性元件受力增加、位移增加，钢丝绳股与股之间的摩擦力增大，局部出现滑移，这种状态下，联轴器的阻尼成分以粘性阻尼为主，摩擦阻尼次之，闭合曲线，即阻尼力曲线的形状呈椭圆形，振幅为2-4毫米。见图（3-9)(b）～（d)，随着联轴器受力的进一步增大，位移随之增加，钢丝绳股与股之间出现大的相对滑移，阻尼力曲线的形状呈棒缒形，介于椭圆与矩形之间，但更加接近矩形，这说明此种情况下，联轴器的阻尼成分以干摩擦阻尼为主，粘性阻尼为次，振幅介于5-8毫米之间，见图（3-9)(e）～（h)。
(2).表3-1列出阻尼成分函数n（A,f）在1赫兹时，随振幅变化的数值，对应于图3-9中各闭合曲线。
从表中可以看出，当n（A,f)>1时，阻尼成分以“高次”阻尼为主，阻尼力曲线呈橄揽形；当0.6<n(A,f)<l时，阻尼成分以粘性阻尼为主，阻尼力曲线呈椭圆形；当0＜n（A,f)＜0.6时，阻尼成分以干摩擦为主，粘性阻尼次之，阻尼力呈棒缒形；当n(A,f)=0时，阻尼成分将变成纯粹的干摩擦，由n（A,f）的值变化可知，产生这种情况的可能性很小。由此可以知道，阻尼成分函数n(A,f)控制阻尼力曲线的形状。
（3）.从图3～9中各图可知：阻尼力的大小随振动位移x变化而变化，实质上阻尼力的大小随振动速度
的大小变化。在x等于零时，速度最大，所以，阻尼力的绝对值达到最大，在位移x为振幅值A时，速度为零，阻尼力零。
（4）.表3-2列出阻尼函数C（A,f）在1赫兹时，随振幅变化的数值，对应于图3-9中各闭合曲线。从表中可知：随着振幅A的增大，阻尼函数随之增大，这说明了联轴器的阻尼耗能随振幅增大而增大的原因。
表3-1 阻尼成分函数n(A,f)控制阻尼力曲线的形状。
| A（mm） |
1 |
2 |
3 |
4 |
| n(A,f) |
1.376734 |
0.9397465 |
0.7516245 |
0.6414627 |
| A（mm） |
5 |
6 |
7 |
8 |
| n(A,f) |
0.5672612 |
0.5130523 |
0.4712813 |
0.4378568 |
表3-2 阻尼函数C（A,f）随振幅A变化表
| A（mm） |
1 |
2 |
3 |
4 |
| C（A,f） |
6.814558×10-2 |
1.351919×10-1 |
2.018296×10-1 |
2.682031×10-1 |
| A（mm） |
5 |
6 |
7 |
8 |
| C（A,f） |
3.343811×10-1 |
4.004035×10-1 |
4.662969×10-1 |
5.3208×10-1 |
将数学模型（3-57）与数学模型（3-12）、（3-13）、（3-41）进行比较，可知
（1）.数学模型（3-57）中的弹性恢复力模型中有三个刚度函数，而数学模型（3-12）中的弹性恢复力模型中有五个刚度函数，因此前者较后者简单，但精度不如后者。
（2）.数学模型（3-57）中的阻尼力中由于引入了阻尼成分函数n（A,f），因而该阻尼力模型能揭示联轴器阻尼成分的组成和变化规律；而数学模型（3-41）中的阻力模型是在阻尼等效原理的基础上建立起来的，因而不能描述联轴器中复杂的阻尼成分。由此可见数学模型（3-57）和数学模型（3-12）（3-13）（3-41）各自有自己的优点和不足，后者能较好地描述动刚度，前者能较好地描述阻尼。
（3）.数学模型（3-57）在参数辨识时，采用的方法是整体辨识法，即将联轴器的弹性恢复力和阻尼力中的各未知参数放在一起进行辨识，由于一次需辨识的参数较多。若再考虑K7（A)，K9（A），将使辨识难度大大增加，故在（3-57)模型中只考虑了K1（A)，K3（A)，K5（A）。而数学模型（3-12）（3-13）(3一41）的参数辨识，采取的方法是拟合分解法，即将联轴器的恢复力分解成弹性恢复力和阻尼力两个式子，分别对其未知参数进行辨识。
在后面的几章中，为了计算简便些，将采用数学模型（3-12)(3-41)。
3-6 小结
本章在钢丝绳弹性联轴器振动试验数据进行分析和处理的基础上，围绕联轴器的建模和参数辨识作了以下工作：
(1）在Ko等人工作的基础上，发展了一种用于非线性迟滞特性系统研究的拟合分解法。用此法将联轴器非线性恢复力迟滞回线拟合分解成两部分：非迟滞非线性弹性恢复力和纯迟滞非线性阻尼力，为分别研究非线性弹性恢复力和非线性阻尼力的特性创造条件，并将Ko法只能辨识三个阶次动刚度的方法发展为能辨识五个或更多个阶次动刚度，为描述大位移强非线性的迟滞特性提供了可行的方法。
(2）针对联轴器动刚度和阻尼是振幅和频率的非线性函数，但当频率增大到一定值后，动刚度和阻尼仅为振幅的非线性函数的特点，分别提出了不受频率影响和受频率影响的非线性弹性恢复力数学模型和非线性阻尼力模型（3-11）、(3-14）式和（3-18）、(3-21）式。根据对联轴器非线性迟滞回线随振幅和频率变化规律的分析，认为提出的数学模型能较合理和客观地描述非线性弹性恢复力和阻尼力的变化规律。
(3）研究了联轴器阻尼耗能特性，提出了阻尼耗能仅受振幅影响和同时受振幅与频率影响的数学模型（3-38）和（3-43）式。在对联轴器非线性迟滞回线面积（即阻尼耗能）进行数值积分的基础上，经过非线性参数辨识，得出了(3-38）和（3-43）模型中的各参数。从而得到了联轴器阻尼耗能随振幅的增大而增大，随频率的增大而减小的函数关系式。
(4）以联轴器非线性阻尼耗能研究为基础，根据阻尼等效原理，研究并建立了联轴器阻尼仅受振幅影响和同时受振幅和频率影响的数学模型（3-40）和(3-45)，经过参数辨识得出了模型中的各参数，由此弄清楚了联轴器阻尼随频率和振幅变化的规律，在此基础上，建立了联轴器非线性阻尼力的数学模型（3-41）和（3-46）式。
(5）对不受频率影响的非线性弹性恢复力数学模型（3-11）式中的参数进行辨识，得出了五个动刚度函数的表达式（3-27)，分析表明，联轴器的动刚度具有刚度软化的特性，这一特性对防冲减振降噪有利。
(6）对不受频率影响的非线性阻尼力数学模型（3-14）式和受频率影响的非线性弹性恢复力数学模型（3-18）及（3-21）式进行了辨识，由于辨识算法的不合适，未能辨识出各参数，为了解决此辨识问题，有待于寻找新的和有效的辨识算法。对联轴器非线性迟滞特性的分析后，仍认为（3-14）、（3-18）和（3-21）式能合理地描述联轴器非线性弹性恢复力和阻尼力。由于频率影响范围很小，在实际计算中，用非线性弹性恢复力数学模型（3-11）、(3-27）式和非线性阻尼力数学模型（3-41）是完全可行的。
(7）对联轴器试验结果和前面关于联轴器建模与参数辨识工作进行进一步深人分析后，提出了联轴器恢复力新数学模型（3-47)，采取未知参数整体辨识法，用Marquardt非线性参数辨识方法，成功地辨识出了式（3一47）中各参数。模型（3-47）的优点是阻尼成分函数n(A,f）的引人使得它能全面地揭示联轴器中的阻尼情况。
上一页
下一页
