第四章 强非线性系统的频闪—谐波平衡法
4-1 引言
在探索具有非线性迟滞特性元件的系统在简谐激励下稳态响应的求解方法时，我们拟研究以下系统：
M
+
（x，
，A，ω）=Pcosωt （4-1）
式中M为系统质量，P为激励力幅值，ω为激励园频率（x，，A，ω）=1（A，x）+2（A，ω，），1和2分别为上章中的（3-12）和（3-41）式。为研究方便，将（3-12）和（3-41）式代入（4-1）式并改写成以下形式：
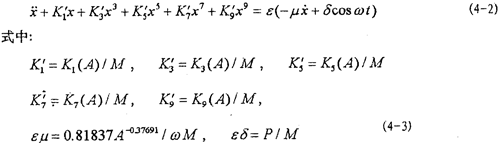
式中K1（A），K3（A），K5（A），K7（A），K9（A）为（3-27）式。由式（4-2）可知，这一系统是一个强非线性非自治系统。
目前文献上的一些方法对于弱非线性系统是有效的，而对于（4-2）式的强非线性系统则遇到了麻烦。由于描述非线性振动系统的微分方程种类繁多，没有普遍的解法，因此，仍然只有极少非线性振动方程可求得精确解。可行的办法是针对不同非线性振动方程的特点寻求一些近似数值解法。为研究方便，将（4-2）式进一步写成以下形式：
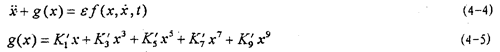
式中：
f（x，，t）=-μ+δcosωt （4-6）
ε为正小参数。
对于形如（4-4）式这样的强非线性系统，李骊提出了一种新的频闪法，近年，杜惠英和李骊用频闪法研究了含有x5项强非线性系统的共振解和亚谐解虽然原则上该方法可适用于任意阶强非线性系统，但是在实际应用中对更高阶项会遇到积分计算问题，大大地限制了这种方法用于高阶强非线性系统的研究。为了解决积分计算的困扰，本章提出一种新的方法—频闪—谐波平衡法。
4-2 频闪—谐波平衡法
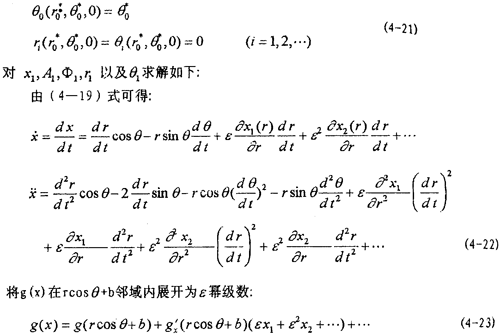
式中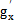
=
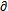g/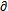x，然后将（4-22），（4-23）及f（x，，t）在rcosθ+b与-rф0sinθ邻域内以ε幂级数展开式代入（4-4）式，由等号两端ε的系数相等得：
式中f=f（rcosθ+b，-rф0sinθ，t），在进行以上积分时f中的时间t 代入以θ表示的函数，求法如下：
因为A1，x1，ф1各式右端均为ε=0时（4-19）中第二式和第三式中ε=0得：
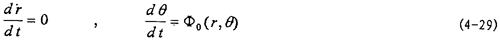
由此两式可求得r=常数，θ=θ（r，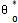
，t）然后可求出反函数t=t（r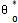，，θ）。由于t式中包含θ0的初值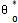，因此由（4-26）～（4-28）式求得的A1，x1，ф1中也必然所含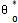，即A1（r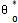，）， x1（r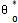，），ф1（r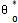，，θ0）。
上一页
下一页
