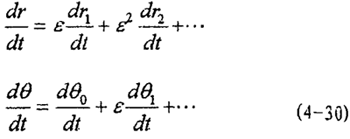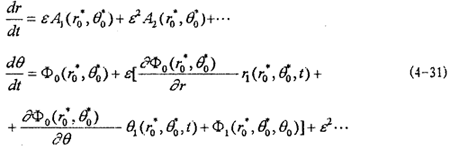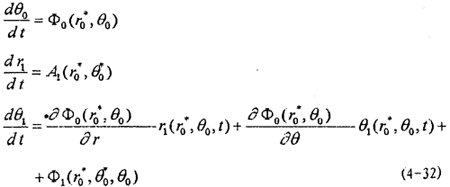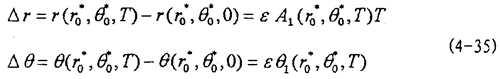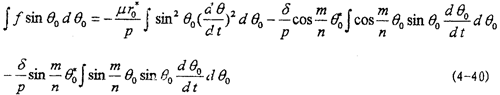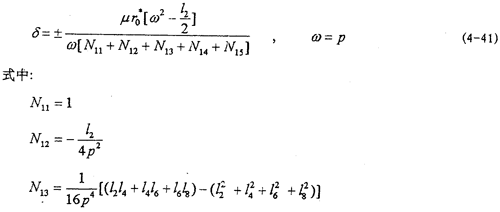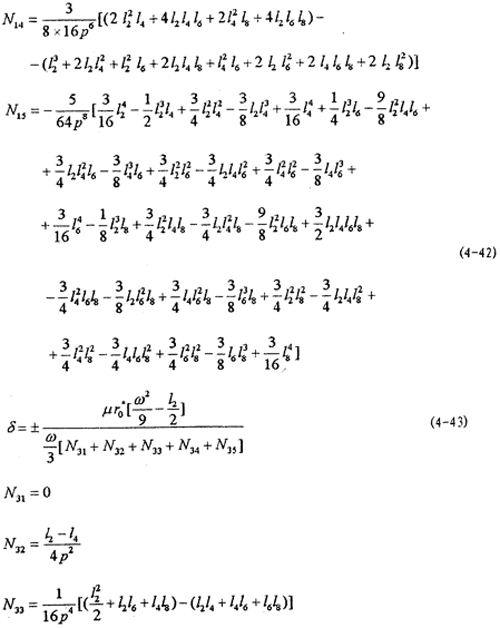为得到（4-2）式的频闪方程，首先由（4-20）求导得：
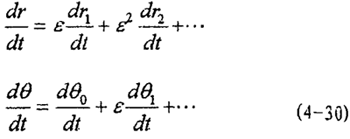
将（4-20）式代入（4-19）式，并将A1，ф1在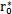
，θ0邻域内展开为ε的幂级数得：
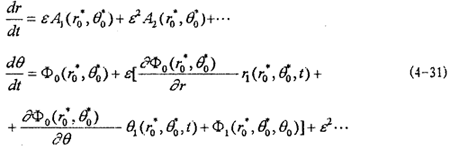
比较（4-31）式与（4-30），由ε的同次幂系数相等得：
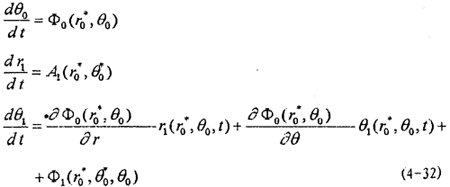
由此可解得θ0=θ0（，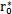
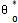，t），反函数t=t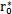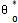（，，θ0），将此式以及（4-20）代入（4-26）～（4-28）式，令等号两端在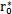，θ0邻域内展开为ε的幂级数并令不含ε的项相等得：
设频闪时间间隔为T=nT0，其中T0为x0=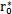cosθ0+b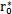（）的周期，n为正整数。于是有θ0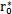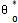（，，T）-θ0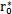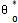（，，0）=0。据此，由（4-20）和（4-34）并略去ε二次以上微量得：
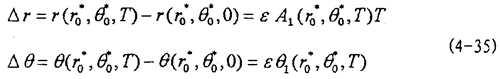
令△τ=εT，则上式化为：
这就是对应于（4-2）式的频闪差分方程，即（4-2）式在Poicare平面上以T为周期的点变换方程。如ε充分小，则可令△τ=dτ，△r=dr，△θ=dθ，此外，（4-36）中的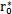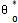，虽为初始值但却可以是平面上任一点（r，θ）于上（4-36）可写成：
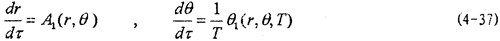
此式就是对应于（4-2）的频闪方程。如果（4-37）存在—稳定—次奇点（r*，θ*），则在此奇点ε邻域内必存在一点（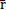
，
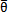），使（4-2）以此点为初始的解为稳定周期解，周期为T，其一次近似表达式为：
在非线性振动系统中，为了求出系统的各次谐共振解，必须考虑（4-15）中各次谐波的影响，为此对以上方法作如下改进：
由（4-15）式可知，-dθ0/dt应为实数，因此，可以证明（4-15）中的
的绝对值小于1。于是可将（4-15）式中的根号部分展开成收敛幂级数。为了将幂级数形式的dθ0/dt引入（4-33）、（4-34）各式进行计算，须对（4-33）中的积分项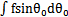
进行变换。利用（4-18）式，得变换如下：
为求（4-2）的各次谐共振，令ω=（m/n）p，其中m，n，为互质整数。于是有：
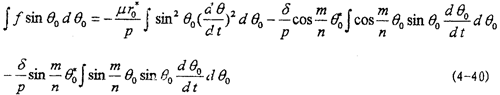
在非线性振动系统中，当系统受到周期性外力作用的情况下，有可能产生三类运动，非共振运动，共振运动，由非共振运动到共振运动的过渡过程，即瞬态运动。对于共振运动来说，有三类，(l)m=n，即ω=p，这是通常所说的共振，称为主共振，(2)n=1，ω=mp，产生泛音共振，当m为奇数时，产生次谐波共振，(3）m=1，ω=p／n，当n为奇数时，产生超谐波共振。将幂级数形式的dθ0／dt代人（4-40)，并计算该式在O～2π区间的定积分，可以得出结论：只有当n=1，m=±1，±3，±5，±7，……时才可能得到（4-2）的周期解，并且（4-2）式只可能产生主共振解和次谐波共振解。
由前面推导可知，系统（4-2）有周期解时，第一个频闪方程dr/dτ=A1（r，0）=0，于是由（4-33）第一式和（4-40）式，再令n=1，m=1，3，5，7可求得（4-2）系统存在主共振解，1/3次谐波共振解，1/5及1/7次谐波共振解时，μ与δ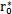，应满足的关系式为：
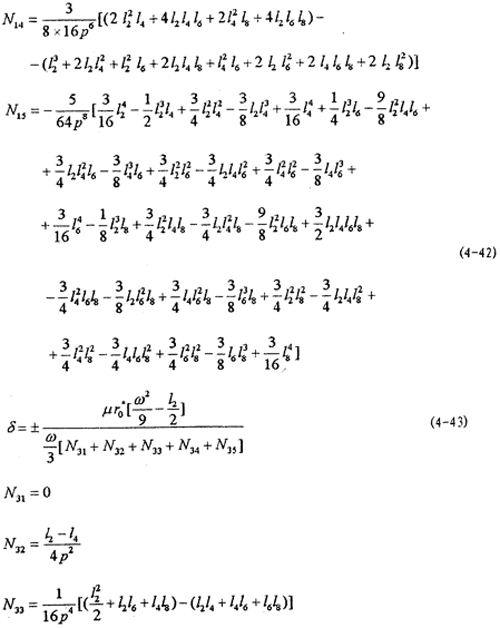
上一页
下一页
