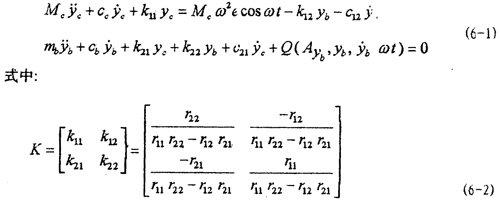第六章 带有非线性联轴器轴系的稳态响应计算实例
6-1 引言
本章将通过一个实例，用SSGILM法计算带有非线性联轴器轴系的强迫振动稳态响应，目的有三：一是验证SSGILM法的有效性；二是考察联轴器对轴系振动特性的影响；三是为下一章试验研究做准备。
6-2 转子轴系力学模型与运动微分方程的建立
本章研究的对象为一个置于外伸轴中的单圆盘转子轴系，如图6-1所示。
圆盘2安装在转轴两支承1的中间位置，轴3一端由具有非线性特性的联轴器4与电动机5联结。转轴的两个支承1中的轴承为双列向心球面球轴承，轴可以在轴承内自由偏转。圆盘靠轴套与轴相联，由于轴套有一定的长度和直径，它对转轴柔度及刚度均有影响，但影响有多大，有待实际计算中考察，故在此先视转轴为一变截面（阶梯）细长轴。同时考虑转轴质量对轴系固有频率的影响。根据第五章建立轴系力学模型的原则，可以将图6-1所示轴系处理成为两个自由度系统，然后根据第五章的式（5-4）、（5-5）可以写出转子轴系的振动微分方程式：
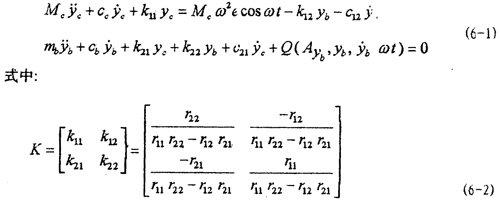
式中的r11，r12，r21，r22为转轴的柔度系数，计算公式见附录1。
yc为圆盘在y轴方向的位移，
c=dyc/dt，
c=d2yc/dt2，分别为圆盘在y轴方向的速度和加速度，yb，b=dyb/dt，b= d2yb/dt2，分别为联轴器从动端质量块mb在y轴方向的位移、速度和加速度。k11，k 12，k 21，k 22为转轴的刚度系数，cc,cb,c12,c21为转轴的阻尼系数，Q为联轴器恢复力。Mc=mc+ms，ms为转轴及轴套的质量，mc为圆盘的质量，ω为转轴的角速度。
6-3 应用SSGILM法计算转子轴系的稳态响应
按第五章提出的SSGILM法及求解步骤，编制了求解转子轴系稳态响应的大型计算机软件，并在386徽机上得到实现。
计算所用的各数据（见附录图1）为：
l=1325mm，l2=45mm，l1=（l-2l2）/2mm，l=30mm
Mc=36.4kg e=0.55mm a=150mm cc=cb=0.001
{a}的初始值任意取为（N=8）：
表6-1 {a}初值表
| a0 |
|
a1 |
 |
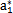a2 |
 |
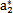a3 |
 |
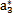a4 |
 |
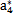| 0.0 |
|
0.5 |
0.3 |
0.4 |
0.2 |
0.1 |
0.1 |
0.08 |
0.07 |
| a5 |
 |
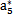a6 |
 |
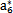a7 |
 |
a8 |
 |
|
|
| 0.06 |
0.05 |
0.04 |
0.03 |
0.02 |
0.01 |
0.009 |
0.0 |
|
|
实际计算表明轴套对轴系振动特性的影响不大，转轴可视为等截面轴。
6-4 理论计算结果分析
将计算所得数据画成曲线，如图6-2（a）～（d）。图中A表示幅值，Ayc表示位移yc的幅值，Ayb表示位移yb的幅值，Ayc1表示轴系振动微分方程形式（6-1）第一式中等号右边恢复力产生的位移yc1的幅值，Ayc2表示式（6-1）第一式中等号右边圆盘质量偏心力激励作用下产生的位移yc2幅值。
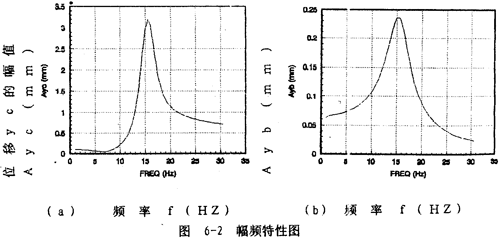
从图6-2（a）可以知道轴系在圆盘质量偏心力激励作用下，圆盘在y方向的振动位移幅值Ayc从1赫兹开始随着频率的增加而有微量减小直至7赫兹，在此之后，位移幅值随频率增大而迅速增大直至轴系的一个固有频率15.56赫兹处，然后位移幅值随频率增大而减小并趋于某一定值。由第五章中的式（5-4）、（5-6）、（5-11）、（5-12）以及本章中的式（6-1）第一式可知，圆盘的振动位移yc是由两部分激励力激励产生的，一部分是Mcω2ecosωt激励力，它产生振动位移yc2，另一部分是（-k12yb-c12b）恢复力激励，它产生振动位移yc1,因此圆盘的振动位移yc=yc1+yc2。
从图6-2(b）可以知道，联轴器从动端质量块mb的位移幅值Ayb从1赫兹开始随频率增大而迅速增大直至轴系的一阶固有频率15.2赫兹，然后随频率增大而迅速减小，在一阶固有频率处达到最大值。
位移幅值Ayc1随频率变化的规律可以从图6-2（c）看到。Ayc1从1赫兹开始随频率增大而增大，在轴系的一阶固有频率处达到最大值，然后随频率增大而减小直至趋于零。Ayc1随频率的变化规律反映联轴器对圆盘振动位移幅值Ayc1的影响部分。
yc2的幅频特性如图6-2(d）所示。Ayc2从1赫兹开始随频率的增大而迅速增大，在轴系的二阶固有频率15.56赫兹处达到最大值，然后随频率增大而减小并趋于某一定值，Ayc2随频率变化的规律反映圆盘仅在质量偏心激励下，而轴系没有钢丝绳联轴器影响时圆盘的幅频特性。考虑上联轴器对圆盘幅频特性的影响部分Ayc1（图6-2(c）所示部分），则圆盘的幅频特性即为图6-2(a）所示。由此可见，钢丝绳联轴器在频率的较低段（0～11赫兹）对圆盘振动有抑制作用。值得一提的是Ayc不是Ayc1和Ayc2的简单相加，而与各频率对应的向量{a}中17个元素以及相位有关。
为了比较各幅频曲线的相对大小以及讨论钢丝绳联轴器对轴系振动特性的影响，画出各幅频曲线相对大小的比较图如图6-3（a）～（b）所示。
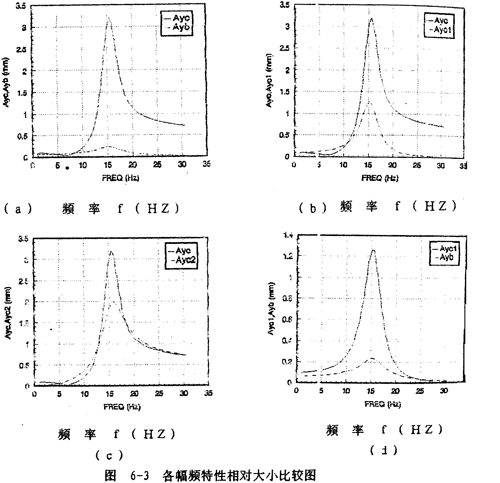
从图6-3（a）可知，联轴器从动端质量块mb的振幅Ayb（虚线）相对圆盘振幅Ayc（实线）来说是很小的。它们各自在一、二阶固有频率处达最大值。
图6-3（b）表示圆盘振幅Ayc（实线）与联轴器引起的圆盘振幅分量Ayc1（虚线）的相对大小比较图。图6-3（c）表示圆盘振幅Ayc（实线）与圆盘质量偏心引起的圆盘振幅分量Ayc2（虚线）的相对大小比较图。图6-3（d）展示了联轴器引起的圆盘振幅分量Ayc1（实线）与联轴器振幅Ayb（虚线）的比较图。从图6-3（b）、（c）可知，圆盘偏心质量引起的圆盘振动位移分量yc2的幅值Ayc2（虚线）大于联轴器引起的圆盘振动位移分量yc1的幅值Ayc1（虚线）。从这两图中曲线的比较还可以知道，钢丝绳联轴器对圆盘振幅的影响在不同频率段效果是不相同的。总的来说，在频率12.7～18.3赫兹区域外，联轴器对圆盘振动是起减振作用的，这一特性可以从图6-13（c）清楚地看到。但在此频率范围内，联轴器对圆盘振动是增大作用的。
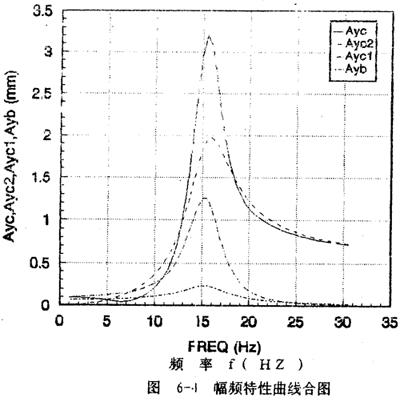
从图6-4各幅频曲线的合图，可以清楚地看到，联轴器从动端质量块mb的振动位移幅值Ayb和联轴器在圆盘上引起的圆盘振动位移分量Ayc1的最大值均出现在轴系一阶固有频率处，而圆盘振动位移幅值Ayc和圆盘质量偏心引起的圆盘振动位移幅值分量Ayc2的最大值均出现在轴系二阶固有频率处，两个固有频率相距较近。
6-5 小结
经过以上实例计算和结果分析可以得出以下结论：
1.用SSGILM法编制的程序从任选的初始值{a（0）}开始进行逼近搜索迭代计算，计算结果表明SSGILM法明显地改变了LM法对初始值要求高的缺点，从任意给定的初始值{a（0）}开始自动逼近搜索，可以很快地收敛于满足精度的{a}值。
2.钢丝绳联轴器对圆盘振动的影响，在不同的频率段有不同的效果，在轴系固有频率附近区域内，钢丝绳联轴器使圆盘振动位移幅值增大，而在轴系固有频率附近区域外。联轴器对圆盘振动具有抑制作用。
3.在整个计算频带，联轴器振动位移幅值相对于圆盘振动位移幅值来说很小。
4.SSGILM法能够计算出轴系的一阶固有频率（对应于联轴器），弥补了多自由度非线性系统不能显式计算（对应于联轴器的）固有频率的不足。
上一页
下一页
