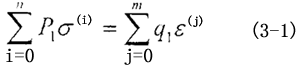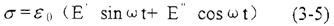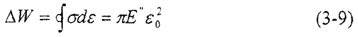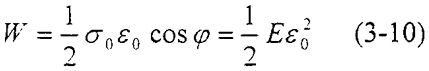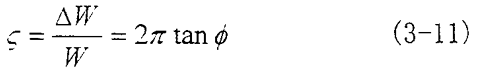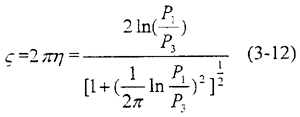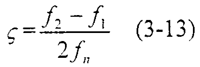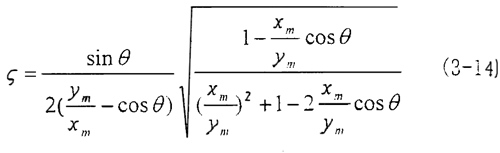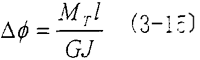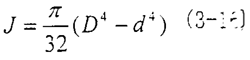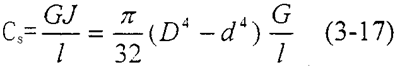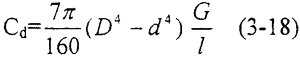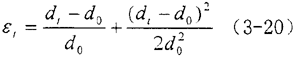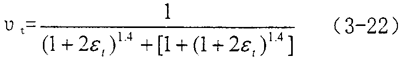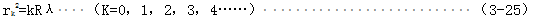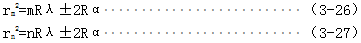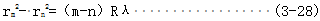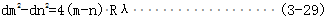|
第3 章扭振的理论计算
3.1 振动的概念
所谓振动,就是物体或某种状态随着时间往复变化的现象。这类现象有的是由于其本身的特性等固有的原因引起的,有的是外界干扰引起的,比如温度,冲击等。在自然界中广泛存在着声、光、电磁波等广义的振动现象。在工程界,地面上的汽车、火车、拖拉机;地下的铁道:天空中的飞机、宇宙飞船;海洋里的舰船、海洋平台等普遍存在着机械振动。在生物界,心脏的跳动,肺的呼吸,肌肉的颤动,脑电波的脉动等等在某种意义上来说,都是一种振动.振动是自然界最普遍的现象之一。
发生振动的机器或结构物等都称为振动系统。实际振动系统往往是很复杂的,因此在开始研究问题时,总要把研究对象以及外界对它的作用简化为一个理想的力学模型、这个力学模型往往由质量块、弹性件和阻尼件组成。质量意味着存在惯性,即系统经过平衡位置时停不下来还要继续往前运动:弹性则意味着质量块要被拉回到平衡位置上。弹性和惯性结合在一起就会发生振动。阻尼元件则使振动受到一定程度的抑制。由此可见,质量块、弹性元件和阻尼元件等是振动系统中的主要元件,它们不同的组合而构成的理想模型可以代替各种实际研究时象。有了这样力学模型,对干理论计算或模拟试验都带来了方便。
3.2 扭转振动的机理
引起弹性联轴器扭转振动的原因主要归结于两个方面:即由柴油机引起的机械扰动和由发电机引起的电气扰动。
3.2.1 柴油机引起的机械扰动
柴油机本身在运行过程中,由于轴系本身不仅具有惯性而且还具有弹性,加上作用在轴系上的周期性的干扰力矩的作用,使轴段产生周向交变及相应的变形,从而使轴系具有扭振的特性。干扰力矩包括柴油机工作时汽缸内气体压力Pg变化而产生周期性的激励力矩,这是引起扭振的主要原因。柴油机曲柄连杆机构运动时的惯性力产生的力矩也是激励力矩的一部分。柴油机运动部件运动时,可产生由重力造成的和有惯性力造成的激励力矩:运动部件的惯性力包括离心惯性力和往复惯性力。离心惯性力是不产生扭振激励的,往复惯性力会产生周期性变化的激励扭矩。
柴油机气缸内工质燃烧期间,气体力是一脉冲载荷,急速燃烧期的压力升高率对其频充特性有重大影响,当出现气缸工作工程故障时,例如进气压力不正常,喷油提前角未调准,燃油雾化质量不良,各缸喷油量不均匀等都会对其他脉冲的起始压力,压力升高率,最高爆发压力,脉冲的作用时间造成影响,使单缸激励力矩的幅值,频率和相位均有变化,导致各缸激励力矩合成结果的变化,而且此时各缸负荷不均匀,各气缸产生的各谐次的激励力矩的幅值和相位彼此不相等,这个也会造成扭转振动。
另外,一些柴油机故障,如燃烧不足、某缸停缸、减振器损坏、曲轴驱动的其它附属系统的损坏等也会产生扭转振动。
3.2.2 发电机引起的电气扰动
包括发电机在内的电气系统,在发生故障或进行某些操作时,电磁力矩可能发生突变或振荡,激起联轴器的扭振。
电力系统中最常见的故障之一就是短路,短路电流可能达到上万安培甚至几十万安培。强大的电流除了产生热和力的作用使电气设备损坏外,还将形成不同频率的扭矩冲击。这是因为在短暂的时间内,柴油机调节系统不可能调整好柴油机和发电机之间的功率,不可能使之达到平衡。短路的类型有三种:三相短路、两相短路和单相短路(或两相接地短路)。前一种为对称短路,出线端三相短路所造成的后果最为严重。后两种为不对称短路。
3.2.3 其他原因造成的扭振动
安装时在联轴器所联接的轴不对中的情况下,会产生一个附加应力,从而产生附加扭矩,造成联轴器的扭振现象。
另外,由于环境的影响或者旋转时候的摩擦,产生大量的热能,热应力也会促使联轴器出现扭振现象,影响联轴器的工作状态和使用寿命。
3.3扭转振动特性模型
在扭转振动特性(包括固有频率和振型)的计算中,常用的模型主要有两种:集中质量模型和连续质量模型。前者又可以分为简单集中质量模型和多单元集中质量模型。
3.3.1 集中质量模型
集中质量模型,是将研究对象分解成若干集中质量块,相邻质量块之间用无质量的理想弹簧联结,形成一种多质量一弹簧系统。根据分块数的多少又可以分为简单集中质量模型和多单元集中质量模型。由于分块数的多少决定着计算的精度,简单集中质量模型虽然可以对研究对象低阶特性进行精确的描述,但由于其本身阶数很低,无法体现研究对象较高频率模态,所以这种模型一般只用作定性分析。多单元集中质量模型本质上与简单集中质量模型相同,但是它根据研究对象的结构特点大大增加了分块数,不仅可以计算研究对象的低阶特性,在计算研究对象高阶特性时也可以有很高的精度。其缺点是当阶数较高时计算量太大,计算耗时长,计算精度也会由于计算中出现的累积误差而降低。
针对这些问题,有关学者提出用各种降阶方法,如最优Hankel范数降阶法、平衡降阶法等,在保证计算精度的前提下,降低模型阶数。也有采用基于最小二乘法和轨迹灵敏度理论的参数辨识法,对给定阶数的研究对象模型进行刚性系数和惯性系数的辨识。这些方法各有优缺点,在不同的程度上解决了高阶集中质量模型的问题,但由于涉及理论较为复杂,有些降阶方法更是以降低精度作为代价的。此外,集中质量模型忽略了某些刚性元件的挠性,不能处理这些刚性元件的复合振动。这些都限制了多单元集中质量模型的应用。
3.3.2 分布质量模型
如果研究对象本身就是一个具有分布参数的连续体,分布质量模型正是其精确描述。这种模型采用偏微分方程的形式表示,既能准确地计算研究对象低阶频率和振型.也可计算高阶频率和振型。还可分析某些刚性元件挠性对扭振的影响。与集中质量模型相比,分布质量模型可以很方便地计算转轴任意截面的内扭矩,适时地搜索出扭应力最危险的截面位置。由于在进行研究对象的分布质量建模时,将附属元件等转化为附加转动惯量加以考虑,因此这种模型可以分析附属元件挠性对扭振的影响。因此在进行扭振响应的精确计算时,可以选择研究对象的低阶分布质量模型。高阶分布质量模型也存在计算量比较大的问题,可以通过模态舍阶降阶法进行降阶处理。近年来有学者提出一种更为精确的低阶分布质量模型一一四端网络模型,此算法简便快捷,通过改进的四端网络模型还可以充分考虑阻尼和附加转动惯量对扭振的影响。
3.4阻尼系数的确定
3.4.1基本模型
对于任意粘弹性材料来说,其一般的本构关系都可写成如下形式:
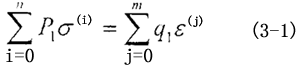
式中σ—应力
ε一应变
σ(i)一应力的i阶导数(i阶应力率)
ε(j)一应力的j阶导数(j 阶应力率)
P1,q1——常系数
从根本上说,橡胶及其增强橡胶材料都具有非线性粘弹性的性质,但非线性方程在工程应用中有很大的困难,故而一般使用线性粘弹性表选形式。
像胶材料在玻璃态转化点附近表现出较好的线性粘弹性,而在较高的温度区内,则表现出强烈的非线性粘弹性。
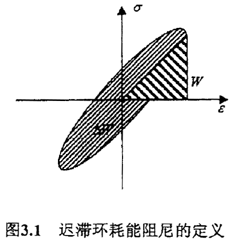
粘弹性材料在简谐波交变动态载荷作用下,应变滞后于应力一个相角φ,因此在一个循环周期内,应力应变迟滞回线为—标准的旋转椭圆,如下图3.1所示,这一椭圆回线的面积△W代表了材料阻尼能力大小,即单位体积耗散的能量,三角形面积W为材料所储存的最大弹性能密度。
若给定应变激励为

则应力响应函数为:

如果以复数形式表征

展开(3-3)式有:
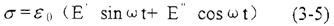
式中E-材料的弹性模量
E-储存模量

E-耗能模量

滞后角

单位体积耗散的能量△W
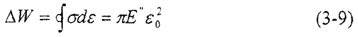
单位体积最大弹性储能
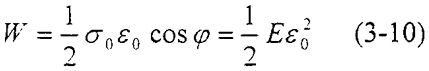
阻尼系数:
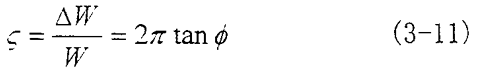
从(3-11) 式可以看出,如果能测出耗能面积ΔW或应变应力的滞后角φ,就可以测定阻尼系数。
3.4.2测量方法
(1)自由振动法测阻尼系数
对于粘弹性材料来说,由于具有粘滞性,其自由振动表现为一衰减波形式。通过分析其峰值包络线,即可得到阻尼系数。
图3.2为自由振动法的测量装置示意图。
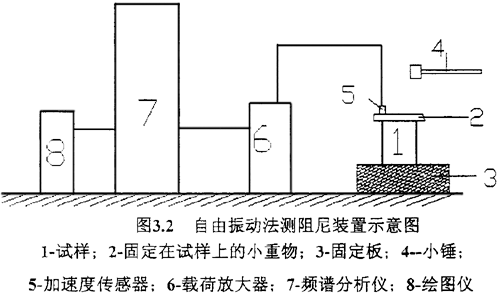
试样在被轻轻锤击所产生自由阻尼振动,其加速度信号通过载荷放大器输入频谱分析仪,经两次积分后得出位移衰减曲线,如下图3.3所示。可得出春滞后阻尼系数。
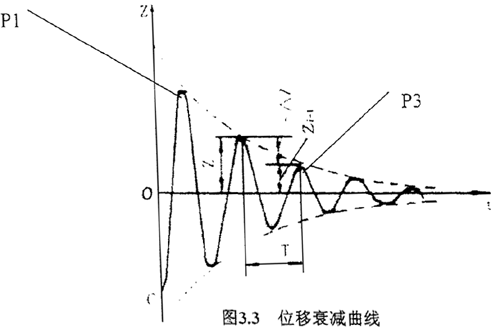
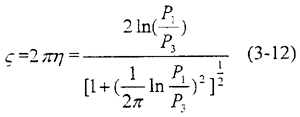
式中P1,P3—图3.3中标明的曲线峰值,ζ称为耗能因子
实际上,由于振动的随机性,其曲线峰值亦具有随机性,滞后阻尼系数可通过最小二乘法求包络线方程y=pexp(-ηωnt)出。式中y为位移,ωn为固有频率。
(2)强迫振动法测阻尼系数
用自由振动法测滞后的阻尼系数时,难以考虑温度及应变率对其的影响。而使用强迫振动法测可计入温度及应变率的影响。对于给定的试样,先预加一初应变,然后加一受控的正弦应变波,使试样做拉一拉运动(始终保持正应变),预应变以保持加载过程中试样不受压力为准。通过这个实验,可以得到材料的应力—应变曲线的滞后圈,并可得到循环加载的次数对滞后圈的影响。根据前文所提出的滞后损失与应变能的关系,即可得到材料的阻尼系数。
(3)半功率点法
由振动理论知,一个振动系统的能量是与其振幅的平方成正比。系统强迫振动的能量在共振点前后能量为共振时能量的1/2处的两个频率f1、f2称为半功率点频率,则此半功率点频率这差值与系统的阻尼比之间有如下关系
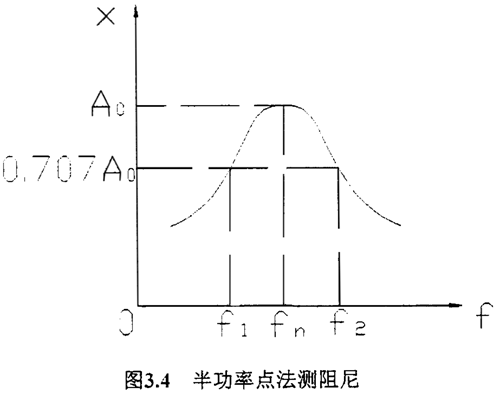
测试件阻尼系数
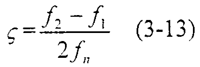
(4)李沙育图法
当被测的阻尼较大时,幅频性曲线和峰值变得不明显或甚至不出现,这时可用李沙育图法。该法的测量系统3.5所示
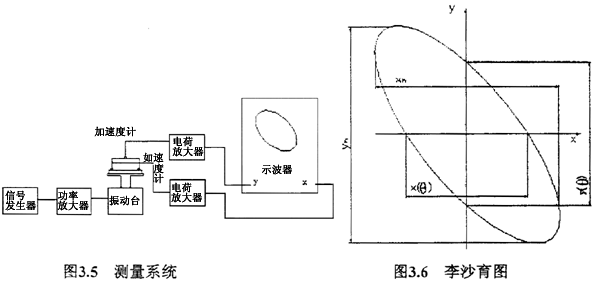
将试件固定在振动台上受激振动。如测振动台面振动的加速度计、电荷放大器和示波器的X轴组成的测量系统与测被测对象振动的加速度计、电荷放大器和示波器y轴组成的测量系统,两者在幅频特性和相频特性上完全一致。
则试件阻尼系数
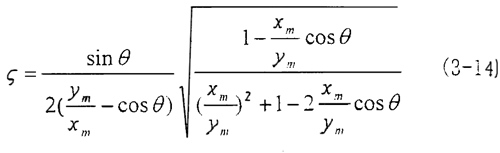
参考前人的研究数据和以上的实验方法,再综合实际测量的结果,我们将橡胶联轴器的阻尼系数定为0.2。
3.5动刚度的确定
从材料力学中可知,对于一根等截面长度为1,材料的剪切模量为G的圆柱轴段,当两商加一扭矩MT时,则轴段两端的盯对扭转角位移为:
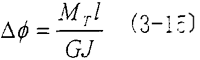
式中J——模截面的极惯性矩,对于空心圆轴状的元件
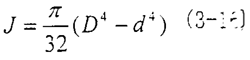
式中D—空心圆截面半径m
d—空心圆截面内径m
材料的扭转刚度表示等直径轴扭转单位角度所需要的扭矩,用CS表示,则:
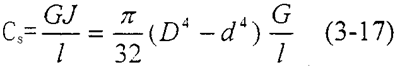
前面介绍过,在弹性联轴器转动过程中,起作用的是动刚度,根据第二章讨论的结果,我们取动倍率为1.4,用Cd表示动刚度,则
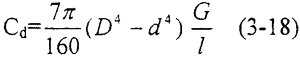
3.6 泊松比的确定
3.6.1 泊松比的定义
泊松比又称横向变形系数,在弹性范围内,材料不论受拉或受压,其值等于侧向应变与轴向应变之比值,用υ表示,即

泊松比无因次量,是表示材料物理性质的一个弹性常数。它是以法国力学家S.D.Poisson (1781-1840)命名的。
3.6.2 泊松比的测量
由于橡胶材料刚度较小,采用接触式的测量方法会增加橡胶表面刚度,使橡胶拉伸变形失真,给材料的应变测量带来很大的误差。因此采用传统的电阻应变片法和云纹法等接触式测量方法已经不能准确地测定橡胶材料的拉伸变形。非接触式变形测量方法很多,拉曼光谱法、电子散斑干涉法、中子衍射法等方法也已经被采用,还有采用高分辨率的电荷耦合传感器(CCD)的3D 光学非接触式变形测量仪测量三维变形。
(1)电荷耦合传感器(CCD)
在橡胶单轴拉伸实验中,选用十字形试样。橡胶试样工作区域尺寸为50mm×50mm。在试样的前后两面各划2条距离20mm的平行白色标记线,白线的中心位置用一维质心法来确定。以此作为靶标,通过CCD测量系统比较不同时刻平行的2条白线的质心之间位移的变化
在橡胶试样拉伸过程中,首先通过长距显微镜将t时刻白色标记的位置聚焦在CCD探测器上,得到的两路位移信号通过变换电路变成电压信号后,同时由CCD传感器送入同步驱动器,再由同步驱动器送入12位AD数据采集卡。单向拉伸实验数据以时间-位移的形式被输入计算机,通过数据处理软件系统处理后,就可以得到橡胶在任意时刻的应变和泊松比。
该实验中平行的两条白线中心之间的起始距离(d0)为20mm,拉伸t时刻时两条平行白线中心之间的距离变为d1,设εt为材料在t时刻的格林应变,则
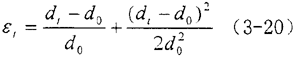
假定如果拉伸方向是1方向,垂直于拉伸的方向为2方向,则橡胶在t时刻的主泊松比(υt)为

假定橡胶材料在拉伸状态时材料变形前后体积不变,并假定在变形前后均为方形,橡胶材料在t时刻时泊松比和格林应变的关系可以通过下式确定
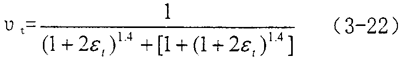
由上式可以看出橡胶材料的泊松比随格林应变的增加而减小。
(2)光干涉式测量
如下图3.7所示,在A、B两支点上,放一截面为矩形,长度为L的试件,两端加外力F(集中力),使试件产生无损弯曲。
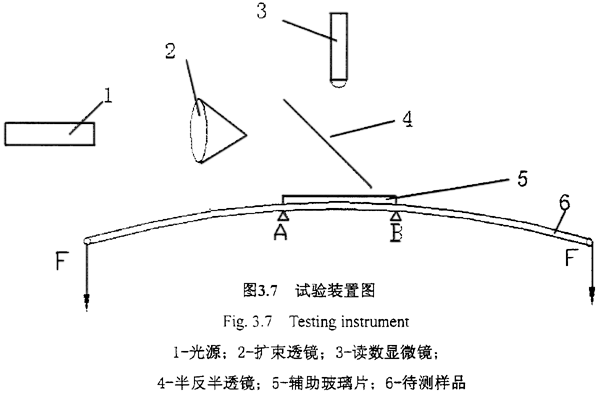
如下图3.8所示,设ρ1表示试件中曲面与xoy面相平行的曲率半径,ρ2表示试件中曲面与yoz面相平行的曲率半径,试件在纯弯曲时沿X轴、Z轴的线应变为
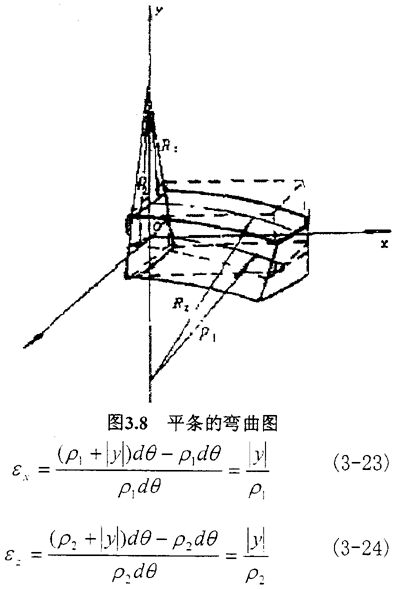
图3.9是轴向弯曲剖视图
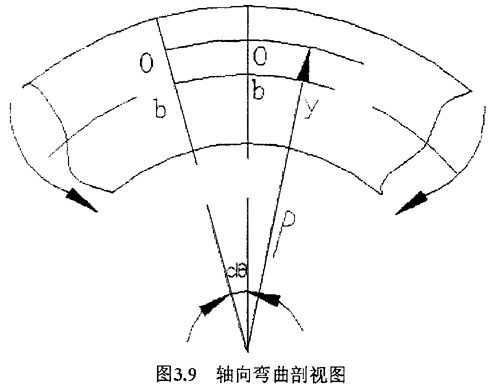
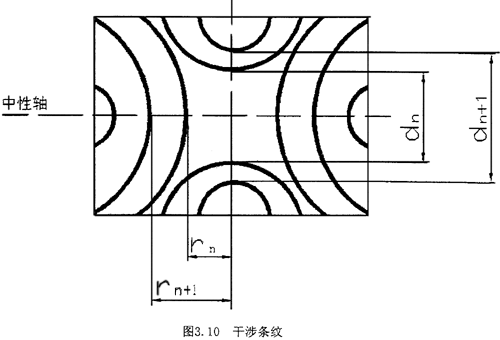
在干涉式测量系统中,辅助玻璃片与变形的试件表面间形成一层薄膜。当光源经扩束透镜和半反透射镜垂直照射时,入射光将在些薄膜上下表面反射,产生具有一定光程左的两束相干光,产生一系列明暗交替的双曲线,在计数显微镜中将观察到双曲线等厚干涉条纹,如图3.10所示。
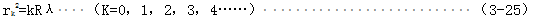
式中rk——第k级双曲线干涉条纹顶点至中心线的距离m
假设附加厚度为n,取第m,n级暗条纹,则对应的双曲线的顶点到中心线的距离为
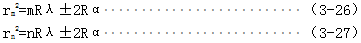
式中rm,rn—第m级、第n级双曲线顶点到中心线的距离m
(3-27)-3-28(得)
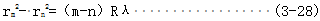
为消除干涉图样中心的确定而产生的误差,转换为对应的双曲线干涉条纹两顶点间的距离的测量,得
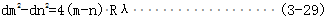
因而轴向弯曲的曲率半径为
上一页
下一页
|