|

同理,横向弯曲的曲率半径为

同薄板纯弯曲理论可知,当应力不超过极限时,材料的泊松比为横向应变与轴向应变之比

将(3-23),(3-24)代入(3-32)可得

(图3.8)设待测试件的厚度为h.则

由于ρ1>>h/2,ρ2>>h/2,所以有:

经过试验和对考国内外相关文献,泊松比υ定为0.4997。
3.7剪切模量和弹性模量的确定
橡胶材料的切变模量G与材料的牌号和组成成分几乎无关,而与橡胶的硬度有关,一般可由以下公式计算:

式中HS——邵氏硬度
e——自然对数的底
该课题所研究的弹性联轴器的橡胶元件的硬度为70,根据式(3-37),剪切模量G=425Mpa。
橡胶材料在拉伸和压缩的作用下,载荷与变形间关系为非线性,但当应变在±0.15范围内,可将应力和应变的关系近似表示为:σ=Eε。别外由材料力学我们可知,弹性模量E和切变模量G之间的关系为:

联轴器各参数如下表3-1所示
表3.1 联轴器参数
| 剪切模量GMpa |
弹性模量EMpa |
动刚度k |
阻尼比η |
泊松比γ |
| 425 |
1274.7 |
1.4 |
0.2 |
0.4997 |
3.8 固有频率的计算
阻尼的存在主要影响轴系发生扭振时各联轴节的扭矩变化曲线和扭振振幅衰减过程,对轴系的疲劳寿命消耗起着重要的作用,但对固有频率及振型的确定影响不大。国外有学者对无阻尼及考虑阻尼两种情况下的大机组轴系扭振特性进行了计算与实测对比,发现二者之间的差异很小,因此在进行扭振特性的振动频率理论分析和实验验证中可以不记入阻尼的影响。
首先进行等效处理,将联轴器两端铁圈的转动惯量等效均布到中间橡胶元件的轴上。等效的原则是转化前后系统总的转动惯量不变。图3.11中b的虚线表示等效后的均布载荷。

假定等效后b的断面在扭转过程中保持为平面,断面原来任一半径仍保持为直线。
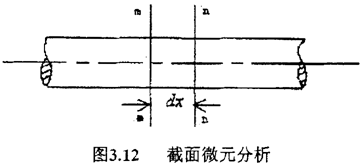
由两个相邻正截面在轴上取微元dx,如图3.12 ,记θ(x,t)表示在t时刻在位置x处截面扭转角。则作用在微元dx的面mm上的扭矩为

在面nn上的扭矩为:

式(3-39),(3-40)中,G—材料的剪切模量
JP—轴断面的极惯性
K—动倍率
微元dx的转动角加速度为:

此时系统单位长度上的转动惯量为:

式中ρ—材料的密度kg/m3
I1——大铁圈转动惯量N·m·s2
I1——小铁圈转动惯量N·m·s2
l——橡胶轴的长度m
联微元dx.由牛顿力学定律得微元段转动微分方程式
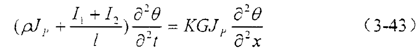
令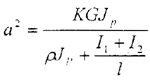 代入式(3-43)并整理上式,有: 代入式(3-43)并整理上式,有:

此微分方程解的形式必为:

将式(3-45)代入式(3-44),得解:
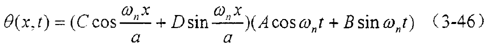
式中A,B和C,D——积分常数,可以通过边界条件加以确定,对于两端自由的轴,端面扭矩为零,
ωn——固有频率
橡胶圆轴两端边界条件为:

联轴器橡胶圆轴件长度为55mm、大的铁圈外径为362mm,内径265mm,小的铁圈外径322mm,内径190mm,内部橡胶件外径298mm,内径265mm。固有频率计算结果分别如下3-2所示:
表3.2固有频率
| 一阶频率hz |
二阶频率hz |
三阶频率hz |
四阶频率hz |
| 45.17 |
90.34 |
135.51 |
180.68 |
3.9扭转振动动力特性计算
假设主动端有稳定转矩T0和扰动转矩Td2sinωt,设稳定转矩产生的转角为φ1,扰动转矩产生的转角为φ2,则主动端和从动端的相对转角φ0为稳定扭矩和扰动扭矩产生的转角之各,即有:
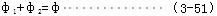
由材料为学可知:
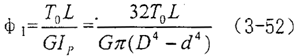
式中L——联轴器长度m
G——联轴器材料的剪切模量,mpa
IP——截面极惯性矩m4
D——套筒的外径m
d——套筒的内径m
现单独考虑扰动转矩产生的相对转角φ2,目前国内建立了图3.13所示力学模型[2],出于橡胶件相对于两侧的铁圈刚性很小,现假设:(1)只有联轴器两侧的铁圈具有刚性,只有橡胶具有弹性和阻尼;(2)联轴器主动侧作用有按简谐规律变化的扰动转矩分量Tdlsinωt此时按照动量矩定理,按联轴器两侧力矩平衡条件,可以分别列出两个圆盘的转动运动方程式,即系统振动的微分方程是:
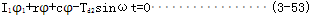
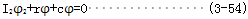
式中φ1——主动圆盘的转角rad
φ2——从动圆盘的转角rad
φ——两圆盘的相对转角rad
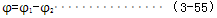
I1,I2——主,从动盘的等效转动惯量N·m·s2
C——联轴器刚度N·m/rad
r——联轴器粘滞阻尼系数N·m·s/rad
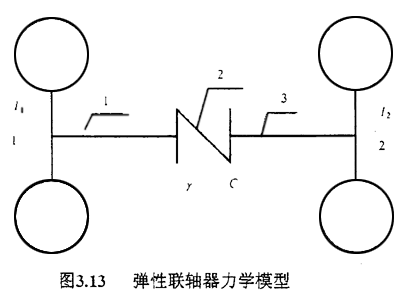
1—主动盘;2—联轴器;3—从动盘

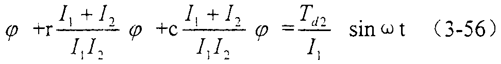
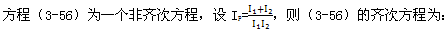

方程(3-57)特征方程为:
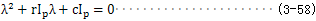
方程(3-58)的解的形式取决于 的值,当 的值,当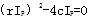 时,(3-58)有两个相同的实根,此时 时,(3-58)有两个相同的实根,此时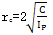 ,称为临界阴阻尼系数。 ,称为临界阴阻尼系数。

当ε<1时,(3-58)有共扼复根,称为欠阻尼情况,方程(3-57)的解为:


得到了联轴器主动端和从动端的相对转角后,就可以得到联轴器内部由于发生扭转产生的应力大小。
当材料力学可知:扭转产生剪应力τ
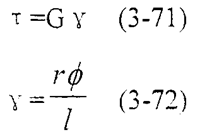
式中G——材料的剪切模量mpa
γ——剪应变rad
φ——相对扭转角rad
r——该处的半径m
l——联轴器的长度m
当联轴器同时受到稳定转矩和扰动转矩时,产生的剪应力则为
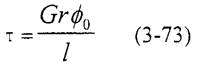
将式(3-68),(3-69),(3-70)分别代入(3-73)可得:

比较式(3-74),(3-75),(3-76)可知,由于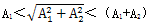 ,所以当阻尼系数等于临界阻尼系数时,产生的剪切应力最小,此时 ,所以当阻尼系数等于临界阻尼系数时,产生的剪切应力最小,此时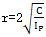 。由于对于一定的材料制作的联轴器,因为材料的阻尼特性是一定的,因此在以后联轴器的设计过程中,可以通过控制两端的转动惯量,或者通过改变联轴器本身的尺寸来控制它的扭转刚度,力求使 。由于对于一定的材料制作的联轴器,因为材料的阻尼特性是一定的,因此在以后联轴器的设计过程中,可以通过控制两端的转动惯量,或者通过改变联轴器本身的尺寸来控制它的扭转刚度,力求使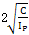 的值尽可能的接近阻尼系数,从而减少产生的剪切力,提高联轴器的工作状态和延长联轴器的使用寿命。 的值尽可能的接近阻尼系数,从而减少产生的剪切力,提高联轴器的工作状态和延长联轴器的使用寿命。
上一页
下一页
|















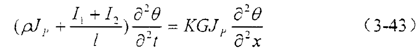
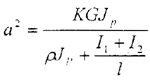 代入式(3-43)并整理上式,有:
代入式(3-43)并整理上式,有:

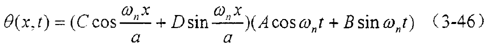

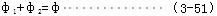
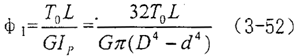
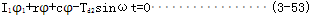
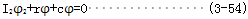
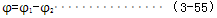


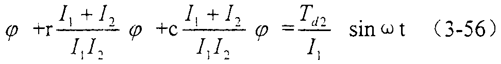
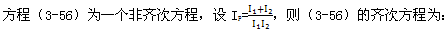

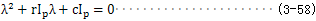
 的值,当
的值,当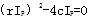 时,(3-58)有两个相同的实根,此时
时,(3-58)有两个相同的实根,此时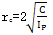 ,称为临界阴阻尼系数。
,称为临界阴阻尼系数。


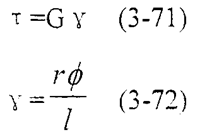
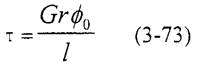

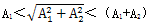 ,所以当阻尼系数等于临界阻尼系数时,产生的剪切应力最小,此时
,所以当阻尼系数等于临界阻尼系数时,产生的剪切应力最小,此时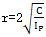 。由于对于一定的材料制作的联轴器,因为材料的阻尼特性是一定的,因此在以后联轴器的设计过程中,可以通过控制两端的转动惯量,或者通过改变联轴器本身的尺寸来控制它的扭转刚度,力求使
。由于对于一定的材料制作的联轴器,因为材料的阻尼特性是一定的,因此在以后联轴器的设计过程中,可以通过控制两端的转动惯量,或者通过改变联轴器本身的尺寸来控制它的扭转刚度,力求使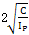 的值尽可能的接近阻尼系数,从而减少产生的剪切力,提高联轴器的工作状态和延长联轴器的使用寿命。
的值尽可能的接近阻尼系数,从而减少产生的剪切力,提高联轴器的工作状态和延长联轴器的使用寿命。