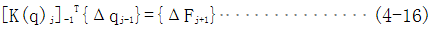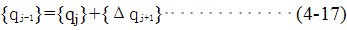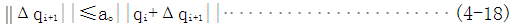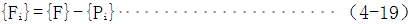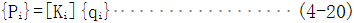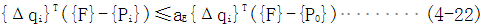|
第4章有限元法分析的理论基础
4.1 有限元基本概念
有限元分析(FEA, Finite Element Analysis)的基本概念是用较简单的问题代替复杂问题后再求解。它将求解域看成是由许多称为有限元的小的互连子域组成,对每一单元假定一个合适的(较简单的)近似解,然后推导求解这个域总的满足条件(如结构的平衡条件),从而得到问题的解。这个解不是准确解,而是近似解,因为实际问题被较简单的问题所代替了。由于大多数实际问题难以得到准确解,用有限元法不仅能提高计算精度,而且能适应各种复杂形状,因而成为行之有效的工程分析手段。
有限元是那些集合在一起能够表示实际连续域的离散单元。有限元的雏形早在几个世纪前就己经形成,但作为种方法而被提出,则是最近几十年的事,例如用多边形(有限个直线单元)逼近圆来求得圆的周长。有限元法最初被称为矩阵近似方法,应用于航空器的结构强度计算,并由于其方便性、实用性和有效性而引起从事力学研究的科学家的浓厚兴趣。经过短短数十年的努力,随着计算机技术的快速发展和普及,有限元方法迅速从结构工程强度分析计算扩展到几乎所有的科学技术领域,成为一种丰富多彩、应用广泛并且实用高效的数值分析方法。
有限元方法与其他求解边值问题近似方法的根本区别在于它的近似性仅限于相对小的子域中。20 世纪60 年代初首次提出结构力学计算有限元概念的克拉夫(Clough)教授形象地将其描绘为:有限元法=雷利-里茨(Rayleigh-Ritz)法+分片函数,即有限元法是Rayleigh-Ritz法的一种局部化情况。不同于求解(往往是困难的)满足整个定义域边界条件的允许函数的Rayleigh-Ritz法,有限元法将函数定义在简单几何形状(如二维问题中的三角形或任意四边形)的单元域上(分片函数),形状(如二维问题中的三角形或任意四边形)的单元域上(分片函数),且不考虑整个定义域的复杂边界条件,这是有限元法优于其他近似方法的原因之一。
对于不同物理性质和数学模型的问题,有限元求解法的基本步骤是相同的,只是具体公式推导和运算求解不同。有限元求解问题的基本步骤通常为:
第一步:问题及求解域定义根据实际问题近似确定求解域的物理性质和几何区域;
第二步:求解域离散化,将求解域近似为具有不同有限大小和形状彼此相连的有限个单元组成的离散域,习惯上称为有限元网格划分。显然单元越小(网格越细)则离散域的近似程度越好,计算结果也越精确,但计算量将增大,因此求解域的离散化是有限元法的核心技术之一。
第三步:确定状态变量及控制方法,一个具体的物理问题通常可以用一组包含问题状态变量边界条件的微分方程式表示,为适合有限元求解,通常将微分方程化为等价的泛函形式。
第四步:单元推导,对单元构造一个适合的近似解,即推导有限单元的格式,其中包括选择合理的单元坐标系,建立单元函数,以某种方法给出单元各状态变量的离散关系,从而形成单元矩阵〔结构力学中称刚度阵或柔度阵〕。
为保证问题求解的收敛性,单元推导有许多原则要遵循。对工程应用而言,重要的是应注意每一种单元的解题性能与约束。例如单元形状应以规则为好,即单元的边长不要相差太大,内角避免出现钝角,避免出现畸形,因为畸形时不仅精度低,而且有缺秩的危险,将导致无法求解。
第五步:总装求解,将单元总装形成离散域的总矩阵方程(联合方程组),反映对近似求解域的离散域的要求,即单元函数的连续性要满足一定的连续条件。总装是在相邻单元节点进行,状态变量及其导数(可能的话)连续性建立在节点处。
第六步:联立方程组求解和结果解释,有限元法最终导致联立方程组。联立方程组的求解可用直接法、迭代法和随机法。求解结果是单元节点处状态变量的近似值。对于计算结果的质量,将通过与设计准则提供的允许值比较来评价并确定是否需要重复计算。
简言之,有限元分析可分成三个阶段,前处理、处理和后处理。前处理是建立有限元模型,完成单元网格划分;后处理则是采集处理分析结果,使用户能简便提取信息,了解计算结果。
4.2 非线性有限元法
非线性有限元法虽然以各类非线性问题作为研究对象,但它脱胎于线性有限元,而且在非线性方程求解时,是将其逐段线性化加以求解。
工业的进步使工程结构越来越复杂,材料品种越来越多,工程结构的工作环境越来越恶劣,对工程结构的效率要求越来越高,因而对结构分析提出了更高的要求。在很多重要的实际问题中,线弹性力学中的基本方程己不能满足需要,应变和位移的关系可能是非线性的,应力和应变的关系也可能是非线性的,变形前和变形后的平衡方程也会发生变化,这就需要考虑非线性因素。
非线性问题可分为材料非线性、几何非线性及边界非线性问题。
材料非线性是指材料的本构关系是非线性的。可分为两类,一类是不依赖于时间的弹塑性问题,当载荷作用以后,材料变形立即发生,并且不再随时间变化。另一类是依赖于时间的粘(弹、塑性)性问题,比较复杂。弹塑性材料的基本特性是:当载荷卸去以后存在不可恢复的永久变形,因而在涉及卸载的情况下,应力应变之间不再存在着唯一的对应关系。
几何非线性是指物体在大变形和大应变情况下,位移与应变的关系不能用线性关系以及小应变假设进行正确的描述,必须考虑变形对平衡的影响或采用大应变理论,这时平衡方程和几何关系都是非线性的。
边界非线性是指由于边界条件的性质随物体的运动发生变化所引起的非线性响应,最典型的例子就是接触问题。
4.2.1 屈服准则
金属材料在变形的过程中,总是由弹性状态过渡到塑性状态。在物体内一点出现塑性变形时应当满足的条件,称为屈服准则或称塑性条件。历史上曾出现过各种不同的关于屈服的假设,通过实验验证,能够应用于工程实际的主要有:屈雷斯卡(Tresca)屈服准则,又称最大剪应力塑性条件:冯· 米赛斯(Von· Mises)屈服准则,又称能量塑性条件。
(1)屈雷斯卡(Tresca )准则
屈雷斯卡做了一系列的挤压实验来研究屈服条件,他认为;当最大剪应力达到某一极限值时,材料即进入塑性状态。这个条件可以写成
当σ1>σ2>σ3时
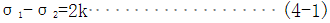
或在一般情况下为
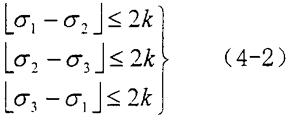
式中σ1、σ2、σ3—互相正交的三个主应力N
k—由材料本身所具有的性质所确定的常数
当上述三个关系式处于不等式的情况下,材料处于弹性状态,如三个关系式中的任何一个处于等式的情况下,材料即处于塑性状态。这个准则称为屈雷斯卡塑性条件。
在材料力学中对于塑性材料常用最大剪应力屈服条件作为强度理论来使用,通常称为第三强度理论。
(2)冯·米赛斯(Von·Mises)屈服准则
屈雷斯片屈服条件不考虑中间应力的影响,另外当应力处在两个屈服面的交线上时,处理时要遇到一些数学上的困难,在主应力方向不知时,屈服条件又很复杂,因此米赛斯在1913年研究了实验结果后,提出了另一种屈服条件。冯·米赛斯准则认为,对于各项同性材料,应力偏量第二不变量等于某一定值时材料屈服。在复杂应力状态下,某点的应力状态由六个分量确定,即以应力分量或应变分量为坐标的空间,空间中每点代表一个应力或应变状态,将处于屈服应力状态下的点连成面即为屈服面,可用应力分量表示
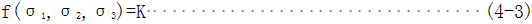
K为与材料相关的屈服极限。应力偏量第二不变量J2达到下式条件时材料屈服
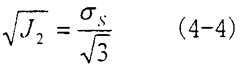
式中σS—材料单轴试验屈服应力N
把一个多维应力状态用单轴应力等效起来,则:

式中σ1,σ2,σ3是三个主应力。上式的几何意义是以σ1=σ2=σ3为轴线的圆柱面。在过原点O 并且垂直于σ1=σ2=σ3的π平面上,屈服函数的轨迹是半径为σS的一个圆周,而在σ3=0的平面上,屈服函数的轨迹是一个椭圆,它的长半轴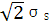 ,短半轴是 ,短半轴是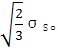
米塞思屈服条件从物理意义上可以解释为:材料的形状改变弹性比能达到某一极限值时,材料开始屈服;或者解释为:当材料八面体上的剪应力达到某极限值时材料开始屈服。在材料力学中,用米赛斯屈服条件作为强度理论使用时,通常称为第四强度理论。
4.2.2 非线性有限元方程的解法
按照解的数学依据进行分类,非线性有限元方程的解法主要有最小化法、迭代法和增量法等。
(1)最小化法
在结构力学中,求解一个结构的平衡问题,通常等于求解结构总位能∏的驻值问题。
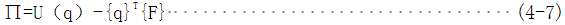
式中U(q)为结构的应变能,而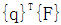 为外载所做功:上式的求解方法之一就是直接数值搜索,即通过数学规划中无约束最小化方法。 为外载所做功:上式的求解方法之一就是直接数值搜索,即通过数学规划中无约束最小化方法。
它的缺陷是:一、往往收敛于局部最小而不是全局最小;二、效率非常低。
(2)迭代法
使用虚功原理使式(4-7)总位能变分为零,得
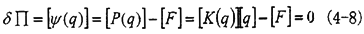
由此可以从第i次的迭代求得i+1次的未知变量{qi-1}
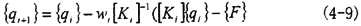
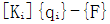 的力学意义为:第i次迭代后的不平衡力,当它等于零时, 的力学意义为:第i次迭代后的不平衡力,当它等于零时,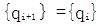 是精确的,当它不等于零时必须迭代求解以逼近精确值。Wi为超松弛因子,用以加速收敛。当式中[Ki]是割线方阵时,称为割线刚度阵,其严重缺陷是收敛性差。如果采用切线刚 是精确的,当它不等于零时必须迭代求解以逼近精确值。Wi为超松弛因子,用以加速收敛。当式中[Ki]是割线方阵时,称为割线刚度阵,其严重缺陷是收敛性差。如果采用切线刚
度阵[Ki]T时就得到牛顿-拉斐逊(Newton-Raphson)迭代法。
牛顿-拉斐逊迭代法的基本思想是:
在t+△t时刻,非线性求解的基本方程为
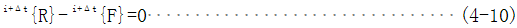
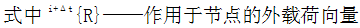
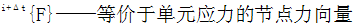
由于节点力和节点位移之间为非线性关系,故必须对上式进行迭代求解,步骤如下
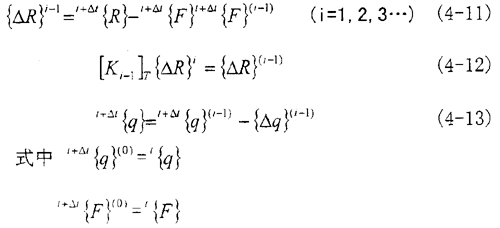
上述方程是根据有限元系统的响应线性化得到的,每一次迭代都是用式(4-11)算小平衡的载荷向量,由这些载荷向量从式(4-10)中导出位移向量,然后继续迭代直至不平衡线荷同量{ΔR}(i-1)或位移向量qi足够小为止。
对切线刚度阵不同的选择方案决定了不同的迭代方法。完全牛顿-拉斐逊法( FullNewton-Raphson)(简称F.N.R)在每一次迭代前都要重新形成[Ki-1]T,并解方程(4-12)。为了节约机时,尽量减少形成[Ki-1]T以及对其进行三角分解的次数,修正的牛顿-拉斐逊法(ModifiedNewton-Raphson)(简称M.N.R)沿用了i=1时的切线刚度阵[K0]T,这样仅形成一次切线刚度阵并进行三角化分解而后的迭代只是线性方程组的回代过程。实际应用修正的牛顿-拉斐逊法时可人为的规定只要进行了一定次数的迭代,就重新形成和分解一次刚度矩阵,以改善[Ki-1]T性质.
M.X.R法在收敛性方面比F.N.R法差,对于逐渐硬化和突然硬化这两种变形硬化的结构,随着载荷的增加,典型位移的增加速度变慢,结构变得更加刚硬,这时用M.N.R法往往会导致发散,即迭代难以收敛。从效率上来说,对于一个软化或轻微硬化结构,达到同一加载步的收敛解的迭代次数,F.N.R法比M.N.R法少,故总的计算时间F.N.R不一定比M.N.R方法多,尤其在非线性程度较高的情况下更是如此。
拟牛顿-拉斐逊法(Quiasi Newton Raphson)(简称QXR)提供了一个介于M.N.R法和F.N.R法之间的折衷办法,在每次迭代中既不重新形成和分解刚度矩阵,又不沿用旧的刚度矩阵,而是用一定的方法对旧的刚度矩阵加以修正并计算新的位移。拟牛顿法给出了第(i+1)次到第i次矩阵的割线逼近,又称割线牛顿法,而量有效的方法BFGS法(Broyden Fletcher Gotdfard Shanno),它结俣了无约束最小化方法给出了最后公式。而字最大的缺点是要占用较多的计算机空间。
比较上述三种方法(F.N.R法,M.N.R法和BFGS法),一般来说,在计算效率上最高的为修正牛顿-拉斐逊法,其次为BFGS法,再次为全牛顿-拉斐逊法;在收敛性力方面情况正好相反,最好的为全牛顿-拉斐逊法,其次为BFGS法,再次为修正,牛顿-拉斐逊法。在结构的分析过程中,当非线性程度不高时(一般为加载初期)用修正牛顿-拉斐逊法,当非线性程度较高时(一般为加载后期)使用BFGS法或全牛顿-拉斐逊法。
为了取得较好的收敛解,在用ANSYS进行计算机模拟的过程中,选用全牛顿-拉斐逊法。
(3)增量法
增量法求解非线性问题时,载荷是一步步逐级旋加的。其前提条件是施加过程中载荷分布是不变化的,可以把某一时刻外载{F}写为λ{F}ref、,λ为载荷乘子,{F}ref为参考载荷矢量,这样增量形式的平衡方程为
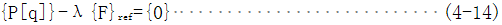
即:
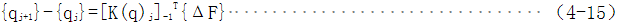
式中增量刚度矩阵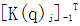 对应于真实变形曲线的梯度,这是增量法的一个优点,它可以追踪结构的变形历史,这对材料与几何非线性(特别是极限屈曲分析)是很有用的。 对应于真实变形曲线的梯度,这是增量法的一个优点,它可以追踪结构的变形历史,这对材料与几何非线性(特别是极限屈曲分析)是很有用的。
最简单的增量法是欧拉-柯西(Euler-Cauchy)法,它在非线性有限元法中称变刚度法,在上述的方程中,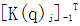 由每一增量步开始时物体的构形计算出,步骤如下 由每一增量步开始时物体的构形计算出,步骤如下
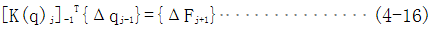
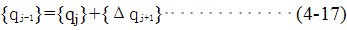
此法普在非线性有限元发展的初期广泛使用,但是期致命的弱点是很快漂移,而不符合实际解,为避免漂移采用平衡修正法可大大提高精度,甚至避免漂移现象。
4.2.3迭代收敛准则
对于方程组的平衡迭代而言,需要一个有效的收敛准则来判断是否结束迭代,用于结构力学的收敛准则主要有三种:
(1)位移准则
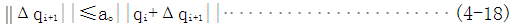
式中aD—位移收敛容差
||Δqi+1||一某种范数,通常取无穷范数、1范数和2范数
在有些时候,位移收敛准则不可靠。
(2)不平衡力(残余力)准则
不平衡力表示为
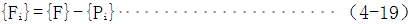
式中{F}——外载荷矢量
{Pi}——第i次迭代终了时与内力相平衡的节点力矢量
静力分析时{Pi}为:
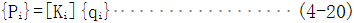
力的收敛准则为

(3)能量准则
本准则的意图在于同时控制位移和力,使之一起处于平衡。方法是把每一次迭代时内能的增量(即不平衡力在位移增量上做的功)同初始的内能增量相比较。
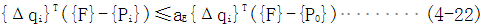
式中aE——预定的能量容差
上一页
下一页
|

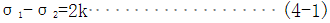
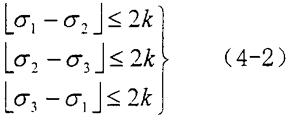
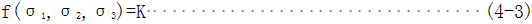
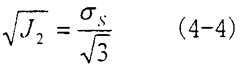

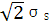 ,短半轴是
,短半轴是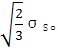
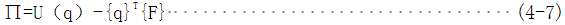
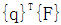 为外载所做功:上式的求解方法之一就是直接数值搜索,即通过数学规划中无约束最小化方法。
为外载所做功:上式的求解方法之一就是直接数值搜索,即通过数学规划中无约束最小化方法。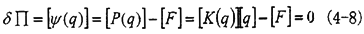
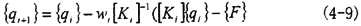
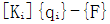 的力学意义为:第i次迭代后的不平衡力,当它等于零时,
的力学意义为:第i次迭代后的不平衡力,当它等于零时,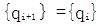 是精确的,当它不等于零时必须迭代求解以逼近精确值。Wi为超松弛因子,用以加速收敛。当式中[Ki]是割线方阵时,称为割线刚度阵,其严重缺陷是收敛性差。如果采用切线刚
是精确的,当它不等于零时必须迭代求解以逼近精确值。Wi为超松弛因子,用以加速收敛。当式中[Ki]是割线方阵时,称为割线刚度阵,其严重缺陷是收敛性差。如果采用切线刚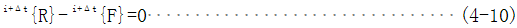
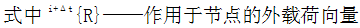
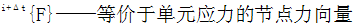
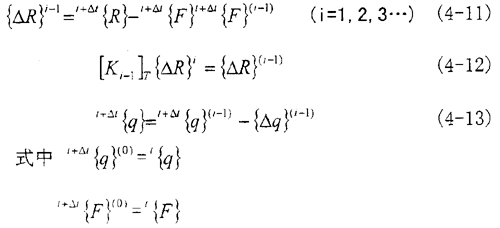
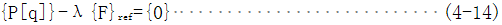
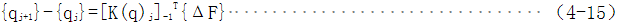
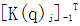 对应于真实变形曲线的梯度,这是增量法的一个优点,它可以追踪结构的变形历史,这对材料与几何非线性(特别是极限屈曲分析)是很有用的。
对应于真实变形曲线的梯度,这是增量法的一个优点,它可以追踪结构的变形历史,这对材料与几何非线性(特别是极限屈曲分析)是很有用的。