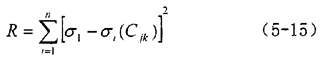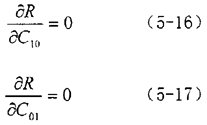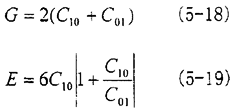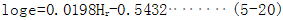|
第5 章弹性联轴器有限元分析
5.1ANSY 概述
5.1.1 ANSYS 简介
随着计算机技术的高速发展,数值计算在工程中已得到越来越广泛的应用,大型的计算软件,如ANSYS已被广泛应用于结构分析、热力学分析、电磁场分析、流体分析、耦合场分析等领域。
ANSYS是一种广泛的商业套装工程分析软件。所谓工程分析软件,主要是在机械结构系统受到外力负载所出现的反应,例如应力、位移、温度等,根据该反应可知道机械结构系统受到外力负载后的状态,进而判断是否符合设计要求。一般机械结构系统的几何结构相当复杂,受的负载也相当多,理论分析往往无法进行。想要解答,必须先简化结构,采用数值模拟方法分析。由于计算机行业的发展,相应的软件也应运而生,ANSYS软件在工程上应用相当广泛,在机械、电机、土木、电子及航空等烦城的使用,都能达到某种程度的可信度,颇获各界好评。使用该软件,能够降低设计成本,缩短设计时间。
ANSYS是由美国ANSYS公司(世界上最大的有限元分析软件公司之一)世界著名的力学分析专家Orswanson率领科技人员多年研究开发。它能与多数CAL软件接口,实现数据的共享和交换。它具有丰富和完善的单元库,材料模型度和求解器.保证了能够高效的求解各类结构的静力、动力、线性和非线性问题、稳态和瞬态热分析及热-结构耦合问题、静态和时变磁场问题、压缩和不可压缩的流体动力学问题以及多耦合场问题。除具有完全交互式的前后处理功能,它还为用户提供了多种二次开发工具,ANSYS 提供的开发工具包括4个组成部分:参数化程序设计语言(APDL),用户界面设计(UIDL),用户程序特性(UPFS),ANSYS数据接口。
到80年代初期,国际上较大型的面间工程的有限元通用软件主要有:ANSYS, NASTRAN,ASKA,ADINA,SAP等。以ANSYS为代表的工程数值模拟软件,是一个多用途的有限元法分析软件,它可广泛的用于核工业、铁道、石油化工,航空航天、机械制造、能源,汽车交通,国防军工、电子、土木工程、生物医学、水利、日用家电等一般工业及科学研究。该软件提供了不断改进的功能清单,具体包括:结构高度非线性分析、电磁分析、计算流体力学分析、设计优化、接触分析、自适应网格划分。它包含了前置处理、解题程序以及后置处理,将有限元分析、计算机图形学和优化技术相结合,已成为现代工程学问题必不可少的有力工具。
5.1.2 ANSYS的基本使用
ANSYS有两种模式:一种是交互模式(Interactive Mode),另一个是非交互模式( Batch Mode)。交互模式是初学者和大多数使用者所采用,包括建模、保存文件、打印图形及结果分析等,一般无特别原因皆用交互模式。但若分析的问题要很长时间,如一、两天等,可把分析问题的命令做成文件,利用它的非交互模式进行分析。
ANSYS 基本对象的构成:
1)节点(Node ) :就是考虑工程系统中的一个点的坐标位置,构成有限元系统的基本对象。具有其物理意义的自由度,该自由度为结构系统受到外力后,系统的反应。
(2)元素(Element) :元素是节点与节点相连而成,元素的组合由各节点相互连接。不同特性的工程统,可选用不同种类的元素,ANSYS提供了一百多种元素,故使用时必须慎重选择元素型号。
(3)自由度(Degree Of Freedom) :上面提到节点具有某种程度的自由度,以表示工程系统受到外力后的反应结果。
5.1.3 ANSYS 架构及命令
ANSYS构架分为两层,一是起始层(Begin Level) ,二是处理层(Processor Level)。这两个层的关系主要是使用命令输入时,要通过起始层进入不同的处理器。处理器可视为解决问题步骤中的组合命令,该软件主要包括三个处理器
模块:前处理模块、分析计算模块和后处理模块。
(1)前置处理(General Preprocessor, PREP7)
这个模块提供了一个强大的实体建模及网格划分工具,用户可以方便地构造有限元模型。ANSYS 程序提供了两种实体建模方法:自顶向下与自底向上。
其过程如下:
① 建立有限元模型所需输入的资料,如节点、坐标资料、元素内节点排列次序
② 材料属性
③ 元素切割的产生
(2)求解模块SOLUTION
前处理阶段完成建模以后,在求解阶段,用户可以定义分析类型、分析选项、载荷数据和载荷步选项,然后开始有限元求解。其步骤为:
① 施加载荷和约束条件
② 定义载荷步并求解
(3)后置处理(General Postprocessor , POSTI1)
POST用于静态结构分析、屈曲分析及模态分析,将解题部分所得的解答如:变位、应力、约束反力等资料,通过友好的用户界面,进行图形显示和数据列表显示。后处理的图形显示可将计算结果以彩色等值线显示、梯度显示、等位移图、等应力图等多种显示方式进行图形输出。
ANSYS 软件提供的分析类型如下:
(l)结构静力学分析:用来求解外载荷引起的位移、应力和力
(2)结构动力学分析:用来求解随时间变化的载荷对结构或部件的影响。
(3)结构非线性分析:对结构非线性导致结构或部件的响应随外载荷不成比例变化的情况。
利用ANSYS软件在计算机上进行有限元件分析的流程图如下图5.1所示:
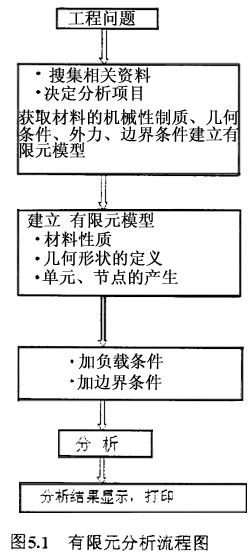
5.2ANSYS建模
该课题研究的弹性联轴器造型如下图5.2:

在ANSYS中建立模型,先通过建立如5.2所式二分之一的剖面图,通过绕中轴线旋转建立模拟模型如下图5.3
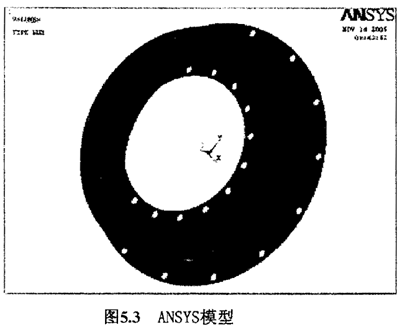
5.3单元选择和网格划分
由于模型是三给实体模型,故考虑选择三维单元,模型中没有圆弧结构,用六面体单元划分网格不会产生不规则或者畸变的单元,使分析不能进行下去,所以采用六面体单元。经比较分析,决定采用六面体八结点单元SOLID185,用自由划分的方式划分模型实体。课题主要研究对象是联轴器中橡胶元件,在自由划分的时候,中间件2网格选择最小的网格,smart size设置为1,两端铁圈的smart size设置为6,网格划分后模型如图5.4。

5.4边界约束
建立柱坐标系R-θ-Z,如5-5所示,R为径间,Z为轴向
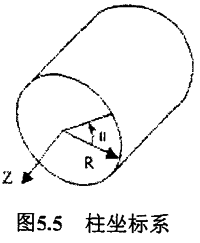
选择联轴器两个铁圈的端面,对其面上的节点进行坐标变换,变换到如图5.5所示的柱坐标系,约束节点R,Z方向的自由度,即节点只能绕Z轴线转
5.5联轴器模态分析
模态分析用于确定设计中的结构或者机器部件振动特性(固有频率和振型),也是瞬态变动力学分析和谐响应分析和谱分析的起点。
在模态分析中要注意:ANSYS模态分析是线性分析,任何非线性因素都会被忽略。因此在设置中间件2的材料属性时,选用elastic材料。
5.5.1联轴器材料的设置
材料参数设置如下表5-1:
表5.1材料参数设置
| |
铁圈1 |
中间件2 |
铁圈3 |
| 泊松比 |
0.3 |
0.4997 |
0.3 |
| 弹性模量Mpa |
2E5 |
1.274E3 |
2E5 |
| 密度kg/m |
7900 |
1000 |
7900 |
5.5.2联轴器振动特性的有限元计算结果及说明
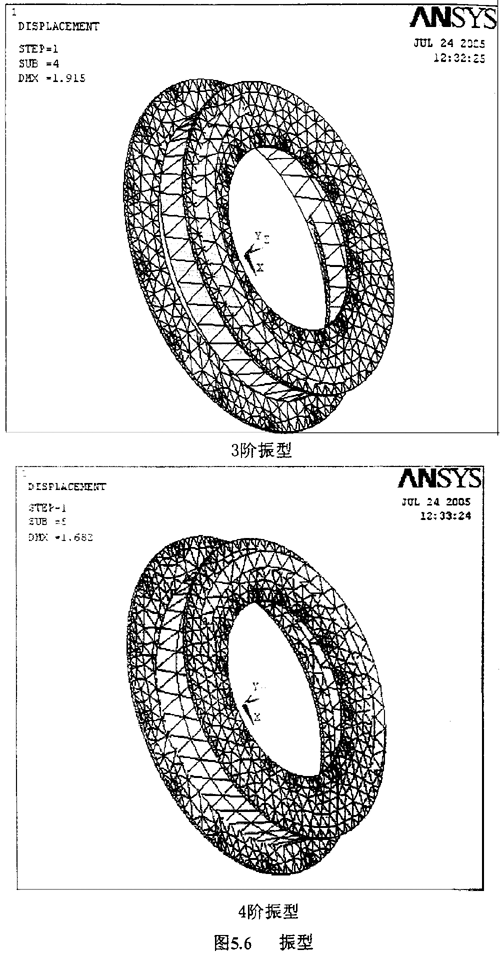
求解方法选择Damped方法,频率计算结果如表5-2,振型结果为图5.6:
表5.2固有频率
| SET |
TEME/FREQ |
LOAO STEP |
SUBSTEP |
CUMULATIVE |
| 1 |
40.199 |
1 |
1 |
1 |
| 1 |
73.632 |
1 |
2 |
2 |
| 3 |
132.42 |
1 |
3 |
3 |
| 4 |
197.34 |
1 |
4 |
4 |
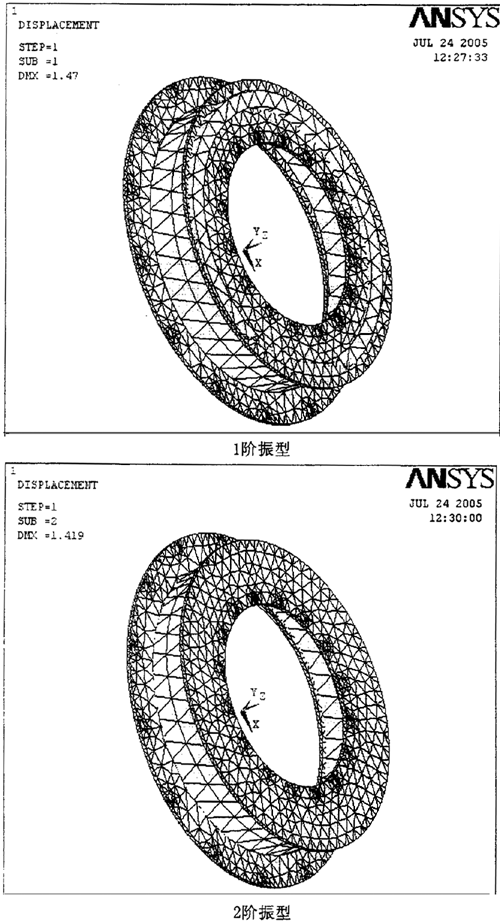
(l)一阶振型
频率为40.199Hz,振型表现为大铁圈和中间件顺时针旋转(从小铁圈观察),小铁圈逆时针旋转。
(2)二阶振型
频率为73.632Hz, 振型表现为大铁圈,中间件和小铁圈同时顺时针旋转(从小铁圈观察)。
(3)三阶振型
频率为132.42Hz,振型表现为大铁圈和小铁圈同时逆时针旋转(从小铁圈看),中间件顺时针旋转,由上图我们可以发现,在这个频率下是联轴器最容易发生断裂。
(4)四阶振型
频率为197.34Hz,振型表现为大铁圈,中间件和小铁圈同时逆时针旋转(从小铁圈观察)。
5.6 联轴器瞬态动力学分析
为了简化计算方法和节省计算用时,首先对联轴器的模型进行简化。因为铁圈上的螺孔的存在会大大的影响计算的复杂程度和时间,但对计算结果的影响却微乎其微,所以决定建模时省略螺孔。简化后的模型网格划分后如下图5.7:
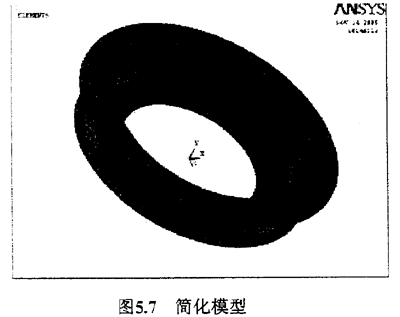
由于橡胶的特殊机械性能,在进行计算机模拟时,必需把非线性因素考虑进去。
5.6.1 非线性分析的基本信息
ANSYS程序应用NR(牛顿-拉斐逊)法来求解非线性问题.在这种方法中,载荷分成一系列的载荷增量.载荷增量施加在几个载荷步.图5.8说明了非线性分析中的完全牛顿-拉斐逊迭代求法,共有2个载荷增量。
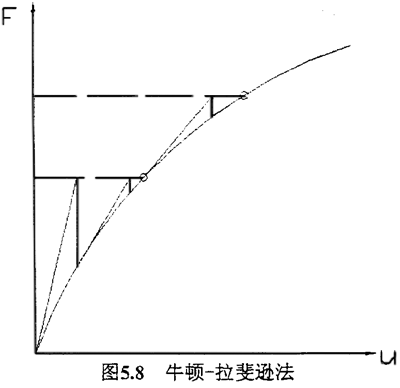
在每次求解前,NR方法估算出残差矢量,这个矢量回复力(对应于单元应力的载荷)和所加载和的差值,程序然后使用不平衡载荷进行线性求解,且检查收敛性.如果不满足收敛准则,重新估算非平衡载荷,修改刚度矩阵,获得新的解答.持续这种迭代过程直到问题收敛。
ANSYS程序提供了一系列命令来增强问题的收敛性,如线性搜索,目动载荷步,二分等,可被激活来加强问题的收敛性,如果得不到收敛,那么程序试图用一个较小的载荷增量来继续计算。
非线性求解被分成三个操作级别:载荷步,子步和平衡迭代.
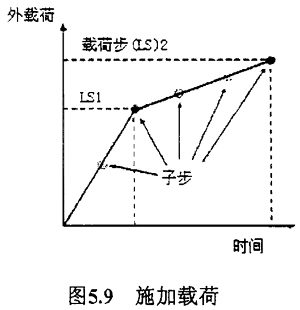
(1)顶层级别由在一定“时间”范围内用户明确定义的载荷步组成.假定载荷在载荷步内线性地变化。
(2)在每一个载荷步内,为了逐步加载,可以控制程序来多次求解(子步或者时间步)。
(3)在每一子步内,程序将进行一系列的平衡迭代以获得收敛的解。
下图5.9说明了一段用于非线性分析的典型的载荷历史。
5.6.2非线性材料的模拟
材料非线性包括塑性,超弹性,蠕变等,非线性应力应变关系是非线性结构行业的普通原因,如图5.10:
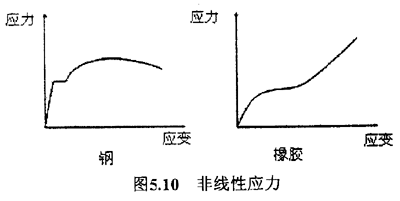
橡胶是高度非线性的弹性体,应力应变关系较为复杂,在本课题中采用工程中广泛采用Mooent-Rivlin2参数模型进行橡胶材料的模拟,参数包括C10和C01。
5.6.2.1Mooey-Rivlin常数测量的理论基础
超弹性材料是指具有应变能函数的一类材料数,对应变分量的导数决定了对应的应力量。应变能函数W为应变或变形张量的纯量函数,W对应变分量的导数决定了对应的应力量,即:
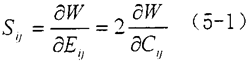
式中Sij——第二类Piola-Kirchhoff应力张量的分量
W——单位未变形体积的应变能函数
Eij——Green应变张量的分量
Cij——变形张量的分量
式(5-1)为超弹性材料的本构关系,可以看出,建立本构关系就是要建立应变能函数的表达式。Mooney-Rivlin模型是1940看由Mooeny提出,后由Rivlin发展的。其中一般形式为
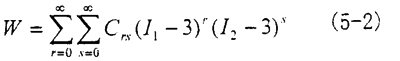
式中Crs——材料常数
I1,I2——Cauchy变形张量的不变量
超弹性不可压缩材料的本构方程可表示为:
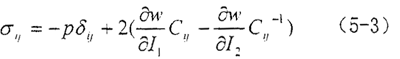
式中σij——Cauchy(真实)应力张量的分量
P——静水压力
δij——Korneker算符
下面假设取变形的主方向为坐标轴方向,则Cauchy变形张量用矩阵形式表示为:
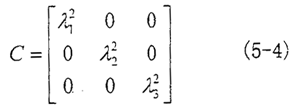
式中λ1——i方向的主伸长比
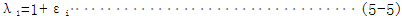
式中εi——i方向工程应变主值
所以Cij的不变量表示为
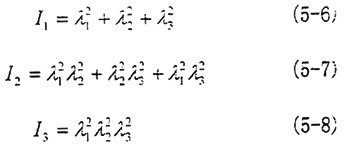
由不可压缩条件: ,考虑薄式片受简单拉伸的情况,即试片一个方向受拉力,另两个方向自由,假设受拉方向为1,则有: ,考虑薄式片受简单拉伸的情况,即试片一个方向受拉力,另两个方向自由,假设受拉方向为1,则有:

给定伸长比λ2=λ,则:
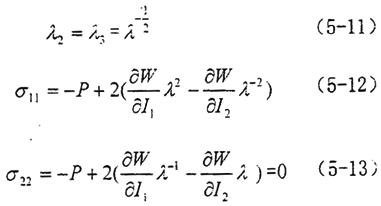
由式(5-13)解出P代入式(5-12)得:
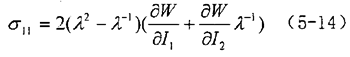
根据所取W的具体形式,可求出 的表达式,其中含有材料常数,由试验数据求得各伸长比及对应的应力,将多个试验点的λ和σ11代入式(5-14),可求得这些材料常数值。 的表达式,其中含有材料常数,由试验数据求得各伸长比及对应的应力,将多个试验点的λ和σ11代入式(5-14),可求得这些材料常数值。
5.6.2.2试验测试
实验采用长的薄式片作为拉伸试样,通过拉伸计算伸长比λ和应力σ。
按式(5-14)进行回归分析,求解回归系数,将式(5-14)中的应力理论值σ11表示为σi(Cjk)(下标i表示数据点序号),用最小二乘法求回归系数Cjk。残差平方和为:
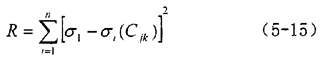
通过对R最小化,求Mooney—Rivlin常数C10,C01。
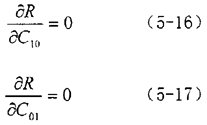
可求得最小二乘意义下的Mooney-Rivlin常数C10,C01。
5.6.2.3橡胶材料的硬度与C10和C01,的关系
G或E与材料常数的关系为
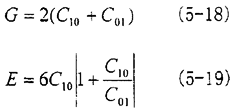
文献给出了橡胶硬度Hr(IRHD硬度)与弹性模量E的试验数据,经拟合得:
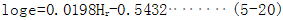
通过硬度利用式(3-38),(5-20)得出G,E,将G,E代入(5-18),(5-19)求出C10和C01。
橡胶的硬度为70,通过计算确定C10和C01分别为1.14Mpa和0.023Mpa。ANSYS中参数设置如图5.11和5.12所示,其中

式中d—橡胶材料的不可压缩比
v—像胶材料的泊松比,0.4997

5.6.3施加载荷
在小铁圈端施加205-105cis314t的动载荷,为了能够清楚地看到动态变化的过程,我们取两个周期。在0.001秒施加第一个载荷,T1=100,迅速达到电动机工作状态。对于正纺载荷,将每四分之一周期划分成五小段,每一个小段作为1个载荷步,一共可分为20个载荷步。载荷点和施加过程如图5.13和图5.14所示:
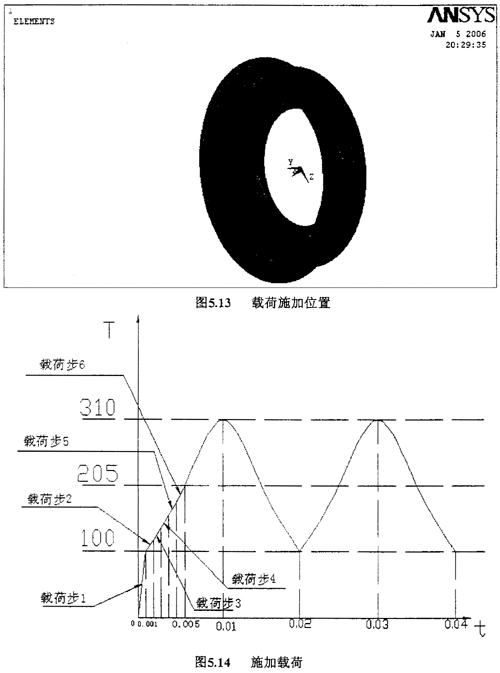
考虑到计算的精确性和计算时间,每个载荷步分成5个子步。
5.6.4计算结果及说明
ANSYS常用的求解器有:波前求解器、稀疏矩阵直接求解器、雅克比共扼梯度求解器(JCG)
,不完全乔列斯基共扼梯度求解器(ICCG)、前置条件共扼梯度求解器(PCG)
前两种为直接求解器,后二种为迭代求解器。本课题采用JCG求解器。计算结果如下图5.15所示:
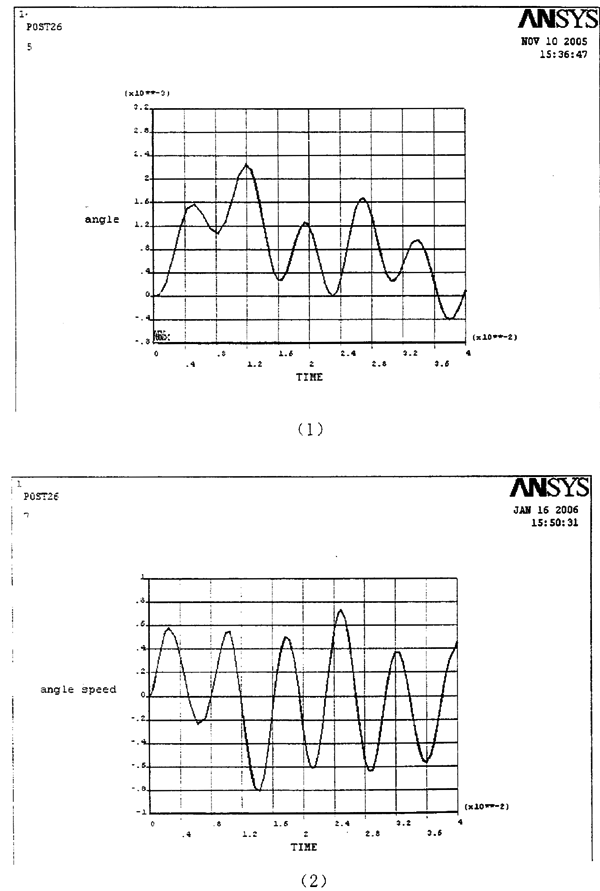
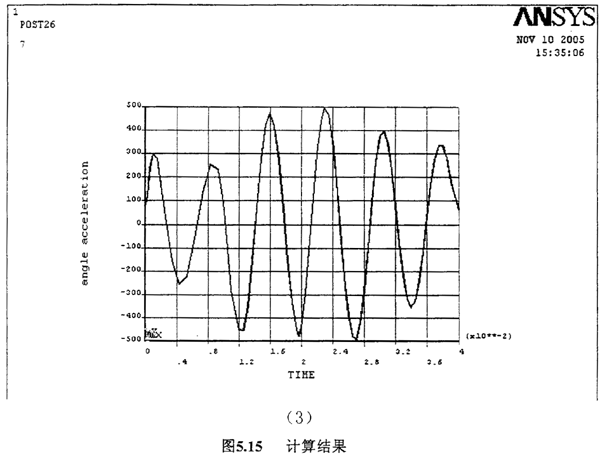
(1)为大小铁圈的相对转角,之所以振幅越来越小是因为理论值中的齐次方程的解随着时间越来越接近于0。(2)为大小铁圈的相对角速度;(3)为相对角加速度。速度和加速度都以类似于正弦曲线发生改变,之所以没有完全按照正弦,是由于阻尼的存在,大大缓解了激励载荷对联轴器的影响。
上一页
下一页
|












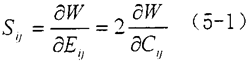
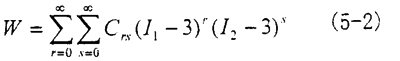
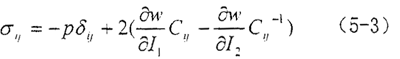
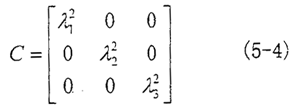
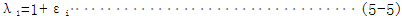
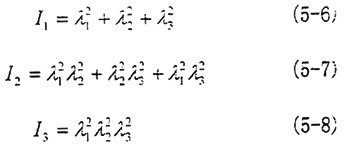
 ,考虑薄式片受简单拉伸的情况,即试片一个方向受拉力,另两个方向自由,假设受拉方向为1,则有:
,考虑薄式片受简单拉伸的情况,即试片一个方向受拉力,另两个方向自由,假设受拉方向为1,则有:
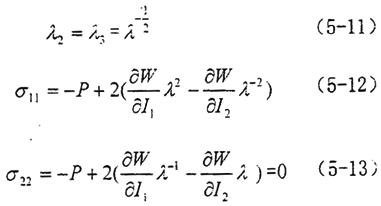
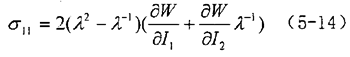
 的表达式,其中含有材料常数,由试验数据求得各伸长比及对应的应力,将多个试验点的λ和σ11代入式(5-14),可求得这些材料常数值。
的表达式,其中含有材料常数,由试验数据求得各伸长比及对应的应力,将多个试验点的λ和σ11代入式(5-14),可求得这些材料常数值。