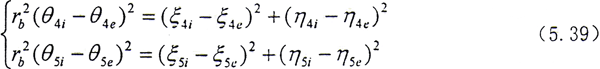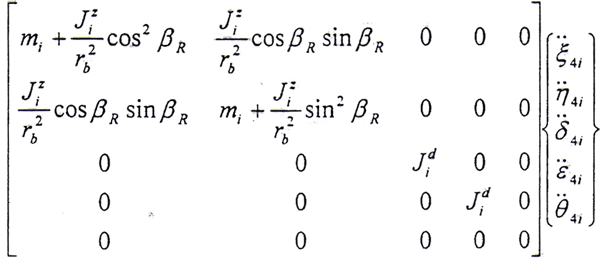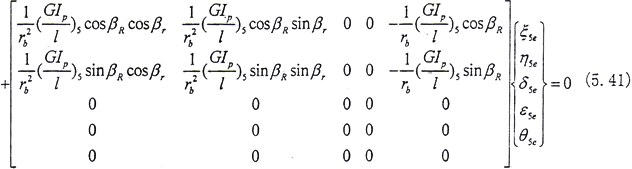5.4 弯扭耦合运动的讨论
(1)在纯扭转情况下,由于内外齿轮的啮合关系表现为传动比是恒定的,即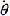 ji/
ji/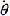 je=1.,虽然这个关系在山内进吾[32]、Marmol[34]和KANEMITSU[38]等人的研究中未曾明确指出,但实质上上式正是他们所处理的齿轮联轴器系统振动问题的出发点,据此将扭转振动和弯曲振动分开处理。
je=1.,虽然这个关系在山内进吾[32]、Marmol[34]和KANEMITSU[38]等人的研究中未曾明确指出,但实质上上式正是他们所处理的齿轮联轴器系统振动问题的出发点,据此将扭转振动和弯曲振动分开处理。
(2)在扭转振动和弯曲振动同时发生时,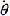 i与
i与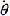 e的关系(参见式(5.11)或式(5.26))不再满足上述关系。从分析力学的角度出发,这个关系实质上是对系统施加了一完整个约束。这个约束关系将表征齿轮扭转的扭转角和表征齿轮质心横向运动的位移联系了起来,正是这个关系才使得弯曲振动和扭转振动耦合了起来。
e的关系(参见式(5.11)或式(5.26))不再满足上述关系。从分析力学的角度出发,这个关系实质上是对系统施加了一完整个约束。这个约束关系将表征齿轮扭转的扭转角和表征齿轮质心横向运动的位移联系了起来,正是这个关系才使得弯曲振动和扭转振动耦合了起来。
(3)从以上推导得的方程式(5.38)可知,轴承—转子—齿轮联轴器系统不仅在弹性项出现耦合,而且存在惯性耦合。从以上的约束关系不难想象,如果考虑了齿轮联轴器的扭转内阻尼,那么此时阻尼项也一定会出现弯扭耦合的现象。因此这是一典型的动力耦合问题。
(4)耦合不仅出现在所考虑的第j个结点上(包括内齿套、外齿轮),而且还影响到j+1个结点上,由于第j+1个结点又与第j+2个结点是耦合的,因此整个系统方程是全耦合的。
(5)虽然质量矩阵和刚度矩阵出现耦合,但在整体系统方程中在齿轮啮合处仍呈现出对称性,这与平行轴齿轮传动系统[18]有所不同,在平行轴齿轮传动系统中质量矩阵和刚度矩阵是非对称的。弯扭耦合的惯性效应体现在对质量阵的修正上,修正项为Jjiz/rb2,设Jjiz=mjiρ2,其中ρ为内齿套的回转半径,一般而言内齿套的质量比外齿轮的质量要大许多,而且内齿套的质量又主要集中在外圈,因此ρ比rb要大,故Jjiz/rb2比mjk,(k=i,e)大得多,这样对质量阵的修正非常明显;弹性耦合由于齿对的刚度较大,而轴的扭转刚度相对要小一些,因此对刚度阵的修正相对要小一些。
(6)弯扭耦合后,运动微分方程只在某些情况下可以进行线性分析,例如在满足βR变化很小等条件,而在一般情况下系统方程则是非线性的,对此将在下一章中进行较深入的讨论。如果将其写成如式(5.38)所示的拟线性形式,则不仅刚度阵是广义坐标的函数,而且质量阵也是广义坐标的函数,这在转子动力学中是比较少见的,因此在讨论此类问题时就非常困难。传统上在进行非线性分析时,往往将式(5.38)写成“状态方程”的形式,由于涉及到质量阵的求逆运算以及方程数目的成倍增加,所以计算工作量是比较大的。
在以往的弯扭耦合振动研究中[16,18,56,101,102,103],主要集中在以下二个方面:1)由于转子系统的不平衡而产生的弯扭耦合现象[56,102]。2)具有外齿轮啮合多平行轴的轴承—转子系统中[16,18,101,103]。由于不平衡产生的弯扭耦合可以通过精细的平衡来消除,从理论上来讲,平衡转子不存在弯扭耦合。而在具有齿轮啮合的多平行轴系统中,弯扭耦合是无法消除的,因此齿轮耦合逐渐成为研究的重点。通过上面的推导,可以发现弯扭耦合在轴承—转子—齿轮联轴器系统中同样存在,而且耦合关系非常复杂,与具有齿轮耦合的多平行轴轴承—转子系统相比,从结构上来看具有明显的不同,在多平行轴的轴承—转子系统中,各转子平行布置一般比较短,扭转刚度大,轴系的扭转固有频率比弯曲固有频率大,此时弯曲振动是转子振动的主要形式。但是在轴承—转子—齿轮联轴器系统中,系统由多个转子串联而成,因此整体系统的扭转刚度成倍降低,轴系的扭转振动问题愈显突出,文献[104]指出在过去的二十年中,在国内和国外均发生过由于扭振而出现大型机组被毁事件。这充分说明了这样一个问题,扭转振动已成为由联轴器连接的轴承—转子系统振动研究中一个不可缺少的内容。因此在轴承—转子—齿轮联轴器系统中进行弯扭耦合振动研究具有重要的实用价值。另外由于弯扭耦合作用,可以对以前未被发现和虽然在实际系统中存在但用传统理论无法解释的振动现象进行深入地研究,以便为此类系统的设计和故障诊断提供必要的理论依据。
5.5 轴承—转子—齿轮联轴器系统的弯扭耦合运动方程
以上我们建立了半联轴器系统的运动方程,而在实际系统中往往是由二对内外齿轮同时啮合传动(例如CL和CLZ型齿轮联轴器),轴承—转子—齿轮联轴器系统如图5.5所示。
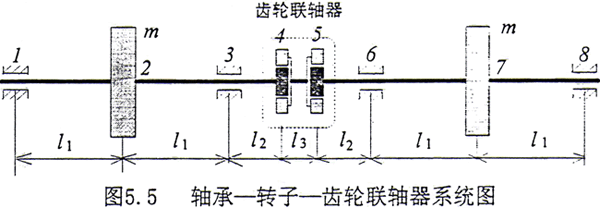
以上系统中有两个半联轴器组成,从上一节的推导中,可以看出在系统中存在二个约束方程,因此系统的自由度数要减少二个。对于图5.5所示系统,在结点4和结点5存在齿轮啮合,因此约束方程为
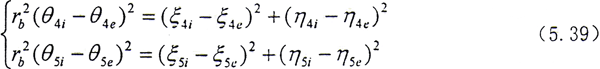
在式(5.27)和式(5.28)中,由于包含了θj+1(即为图5.5中的θ5i)。而θ5i又必须要满足以上的约束关系,所以可以想象在考虑了二个半联轴器后,耦合关系更为复杂。但处理的方法是类同的,具体过程在此不再重复了。整个系统有8个结点,共48个自由度。下面仅列出结点4处的运动微分方程。
结点4外齿轮处


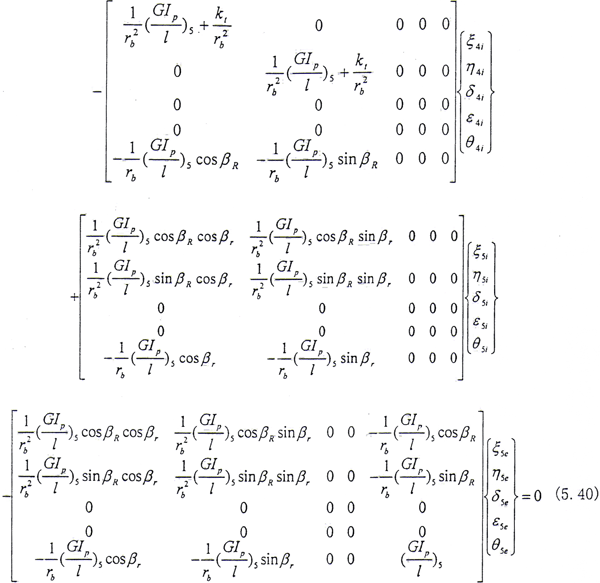
结点4内齿套处
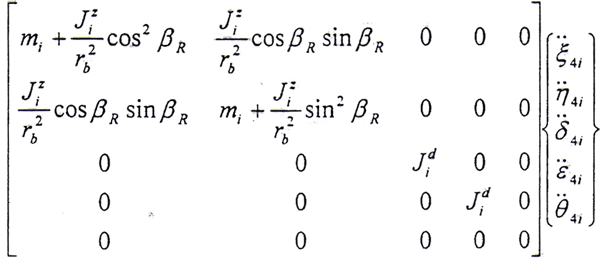
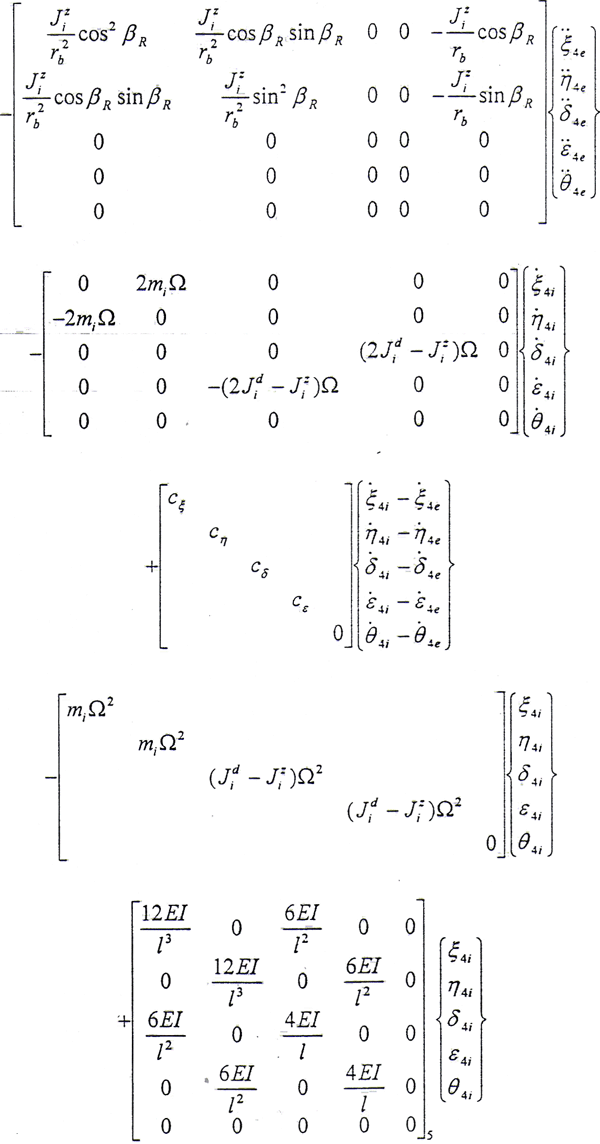
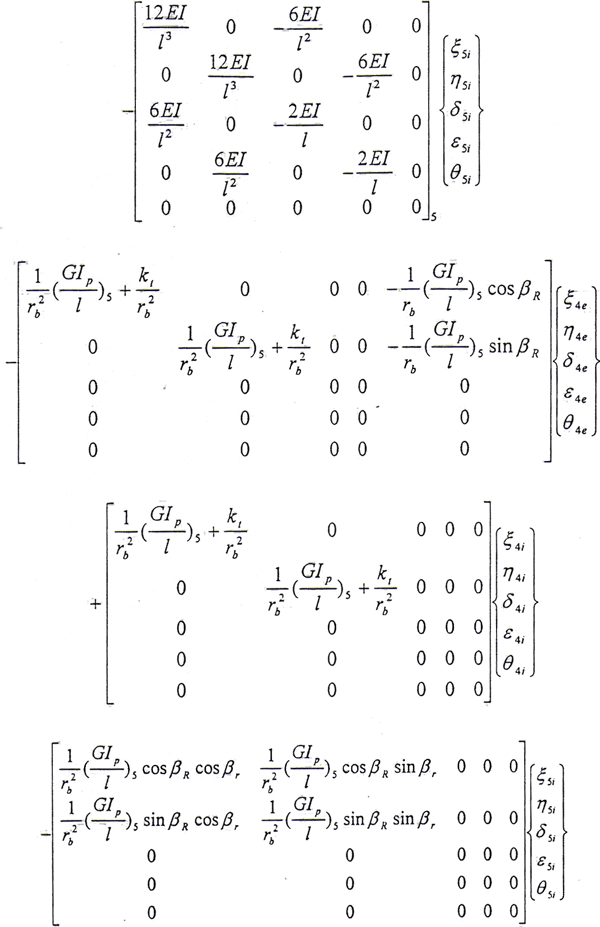
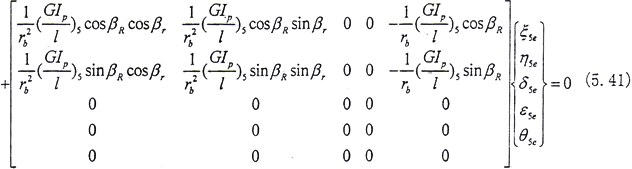
同理可以写出结点5内外齿轮处的运动微分方程,在此从略。
5.6 小结
本章讨论了在联轴器内外齿轮轴线出现不对中或产生动态偏移时,轴承—转子—齿轮联轴器系统的弯扭耦合运动方程的建立过程,并对弯扭耦合进行了简单的分析,主要的工作和结论如下:
(1)根据内、外齿轮的齿面方程和不脱齿的啮合条件,推导了齿轮联轴器的约束方程,这一约束方程体现了弯曲(或横向)位移和扭转扰动角之间的耦合关系。
(2)由拉格朗日方程,在旋转坐标系中建立了半联轴器的弯扭耦合运动方程,并阐述了轴承—转子—齿轮联轴器系统方程的建立过程。
(3)弯扭耦合后,系统不仅存在弹性耦合而且存在惯性耦合,但在整体系统的运动微分方程仍然具有对称性。
(4)建立了CL型齿轮联轴器系统的弯扭耦合运动方程,为深入探讨具有齿轮联轴器连接的轴承—转子系统的动力学行为作了理论准备。
上一页
下一页

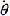 ji/
ji/