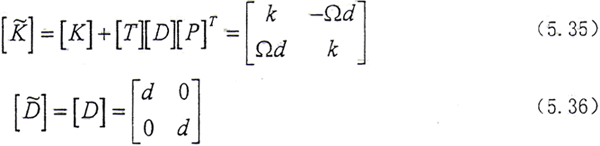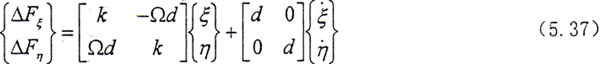第五章 不对中齿轮联轴器系统弯扭耦合振动力学模型
5.1 引言
在第二、第三章推导系统的运动方程时,采用了几个基本假设,其中有一个条件是“联轴器各内外齿承载相同”,这个条件隐含了这样一个事实“内齿套轴线和外齿轮轴线间是在对中的条件下进行线性化的”,这一假设也是被山内进吾[32]、Marmol[34]和Kramer[35]等所普遍采用的。而齿轮联轴器在使用过程中,内外齿轮轴线间有时会出现不对中或产生动态偏移的情况,在这种情况下各齿所分担的载荷要发生变化,按啮合理论[100]二者的啮合关系应为如图5.1所示,此时只有很少的几个齿对啮合(具体由重合度来确定啮合的齿对数)。实际上即使在对中的条件下,如果考虑轮齿的误差也会发生上述情况。日本学者Ssigeo[73]分析了齿轮联轴器轮齿的误差后得出了一套计算公式,通过计算可知,当m=3,Z=56时,其极限情况只有不到4对齿接触。工程实际的分析和试验[63,69]表明,一些采用齿轮联轴器连接的轴承—转子系统会程度不同地产生倍频的振动分量,而这一倍频分量的出现正是齿轮联轴器不对中的典型特征,因此有必要进行相诮的分析。以往在轴承—转子—齿轮联轴器系统的分析中,有关弯扭耦合振动方面的研究未见报道。
本章重点讨论齿轮联轴器内外齿轮轴线间具有动态不对中时系统的建模问题,有关二轴线间存在静态不对中时的情形,我们将在第七章作详细地分析。本章的内容安排如下:首先根据内外齿轮的齿面方程和不脱齿的啮合条件,推导了齿轮联轴器所满足的约束方程,然后由拉格朗日方程,在旋转坐标系中建立了轴承—转子—齿轮联轴器系统的弯扭耦合运动方程,并分析了产生弯扭耦合的原因。
5.2 渐开线直齿内齿轮副(零齿差)传动的运动学分析
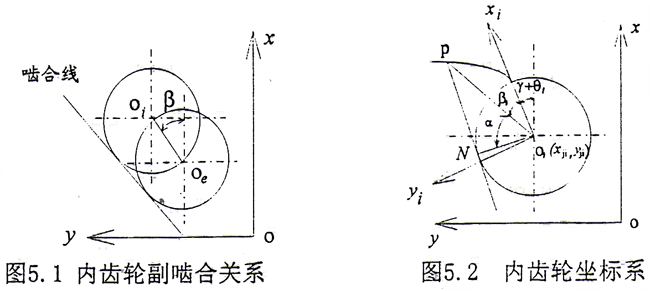
设Si(oixiyizi)坐标系是与内齿套固连的动坐标系,如图5.2所示。xi轴与内齿套某一齿的一侧齿形相交于基圆(半径为rb)上,z轴与内齿套轴线重合,oi为坐标原点。设S(oxyz)坐标系为固定坐标系,则有
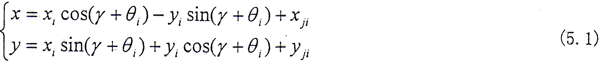
同理设Se(oexeyeze)坐标系是与外齿轮固连的动坐标系,可得
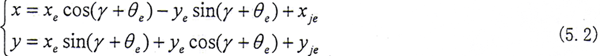
在动坐标系中,渐开线直齿齿面上任意一点P的齿面方程(内齿套)为

式中 γk=α+βk k=i,e
将(5.3)式代入(5.1)式得
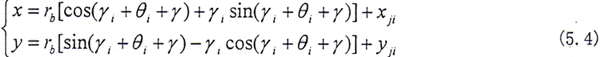
在S坐标系中,内齿套齿面上P点的法线向量和速度分别为
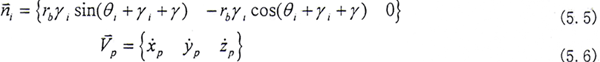
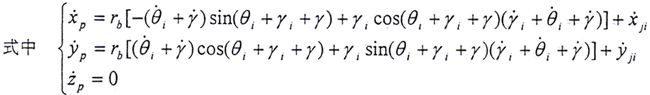
同理可得,外齿轮上p′点的法线向量和速度为
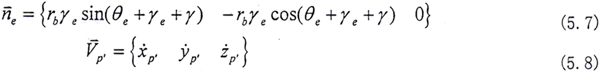
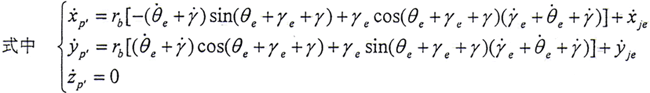
不脱齿轮啮合的条件为
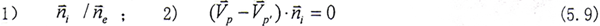
由此可得
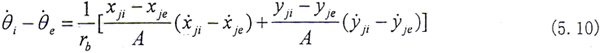
其中:A为两轮中心连线的长度,即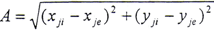
积分(5.10)式即得
(θi-θe)2=[(xji-xje)2+(yje-yje)2]/rb2 (5.11)
设β角是连心线与x轴之间的夹角,参见图5.1,则有

实际上在S系中p和p′的对应坐标应相等,由此可方便地得到
β+π/2=γ+θi+γi=γ+θe+γe (5.13)
上式表明啮合线与连心线是平行的,这一结论与文献[100]相同,这从另一个侧面验证了(5.10)式、(5.11)式的正确性。以上的啮合关系与外齿轮啮合具有类似的形式,只不过在齿轮联轴器中,内外齿轮的基圆半径是相等的。由式(5.13)可以得

在上式中,如果转动角速度Ω是匀速的,并且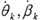 k=i,e是小量时,则
k=i,e是小量时,则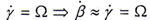 此时,β是以Ωt加上一个微小变化的转角。这样内齿套、外齿轮及二轴中心线的连线均是以轴的转动角速度Ω加上一个微小变化的量旋转的。
此时,β是以Ωt加上一个微小变化的转角。这样内齿套、外齿轮及二轴中心线的连线均是以轴的转动角速度Ω加上一个微小变化的量旋转的。
5.3 半齿轮联轴器系统弯扭耦合的动力学分析
轴承—转子系统动力学方程的建立可参考文献[90],下面主要讨论在齿轮啮合处运动方程的建立。由齿轮联轴器连接的转子系统见第三章的图3.1,由一对齿数相等的内啮合齿轮和左右二段轴组成。设oxyz是固定坐标系,oξηz是旋转坐标系,Ω是圆盘的转动角速度。
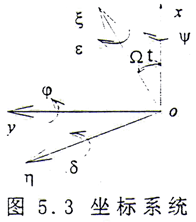
如果将(5.11)式变换到旋转坐标系oξηz中,则有

设
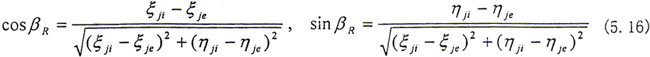
βR表示在旋转轴系中,内外齿轮中心连线与ξ轴之间的夹角。因为
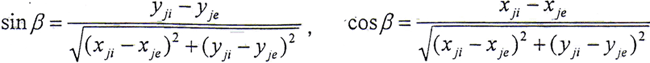
β是内外齿轮连心线与x轴的夹角。
从而可得
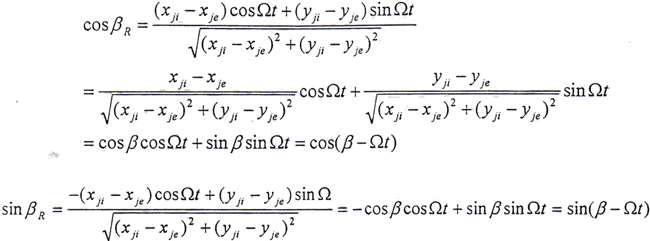
由此可见βR与β相差一个Ωt。
5.3.1 圆盘的运动及其动能计算
圆盘的运动可分解成随其质心的平动和绕质心的转动。质心o1的平动位移为(xc,yc),不计沿z轴方向的运动。圆盘绕质心的转动可用三个欧拉角来表示,如图5.4所示。设o1XYZ是与oxyz平行的坐标系。o1XYZ坐标系的单位矢量为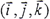 ,o1xmymzm系的单位矢量为
,o1xmymzm系的单位矢量为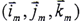 ,(m=1,2,3),则圆盘的转动由如下三个步骤完成:
,(m=1,2,3),则圆盘的转动由如下三个步骤完成:
(1)绕o1Z轴转Θ至o1x1y1z1;
(2)绕o1x1轴转-ε至o1x2y2z2;
(3)绕o1y2轴转δ至o1x3y3z3;
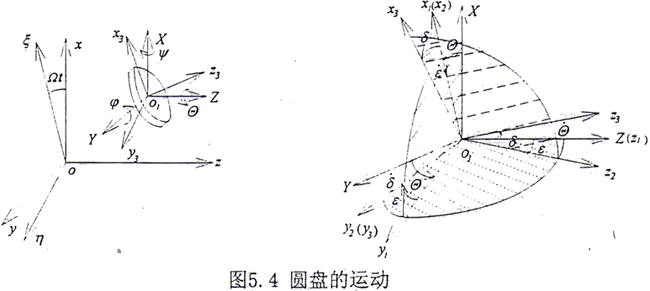
在各坐标系中,单位矢量之间的关系
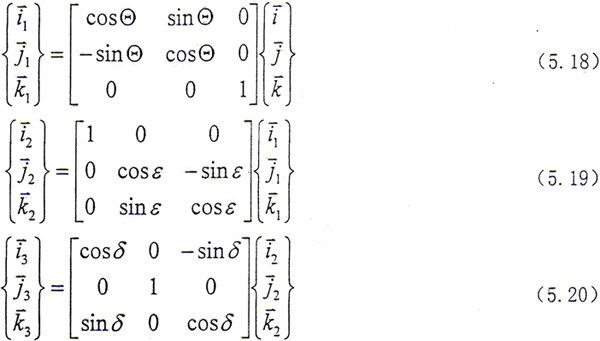
圆盘的转动角速度
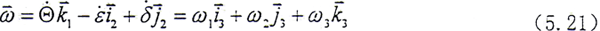
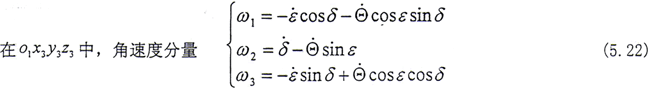
在转子系统中,自转角Θ=Ωt+θ,以上偏角ε,δ,θ,ψ,φ均是小量,则可得出如下关系

圆盘的动量矩
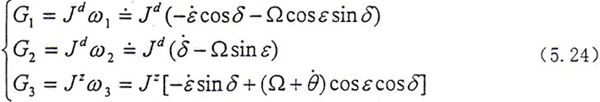
对于圆盘,其动能包括平动动能和转动动能

其中
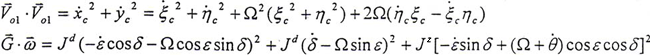
5.3.2 旋转坐标系中的运动方程
在小扰动下满足关系式(5.15),再由式(5.11)和式(5.16)可得
rb2(θji-θje)2=(ξji-ξje)2-(ηji-ηje)2 (5.26)
其中下标变量je、ji分别表示第j个结点处外齿轮和内齿轮。
上式是一个反应齿轮啮合处内外齿轮的扭转扰动角和横向位移之间的约束关系,而且是一个完整约束。对于具有复杂约束关系的多自由度系统,利用拉格朗日方程来建立系统的运动方程具有许多优点,因此被广泛采用。
半齿轮联轴器系统的动能包括内外齿轮的平动动能和转动动能;弹性势能包括左右轴段的弹性势能和半齿轮联轴器的弹性势能;耗散函数包括内外齿轮之间的横向内阻尼和转角内阻尼,由于扭转内阻尼较小可将其忽略,具体的分析过程可参见第三章3.2.2和3.2.3节。这样取q=ξje,ηje,δje,εje,θje,ξji,ηji,δji,εji为广义坐标,将以上的约束方程(5.26)式代入半齿轮联轴器系统的动能,势能及耗散函数中,消去多余的变量θji,再由拉格朗日方程就可以得到在齿轮啮合处的运动微分方程。由于推导过程比较冗长,在此仅列出最终的运动微分方程。对于小偏离情况,将其中的高阶小量略去,则对于第j个结点(其中外齿轮下标为e,内齿套下标为i)


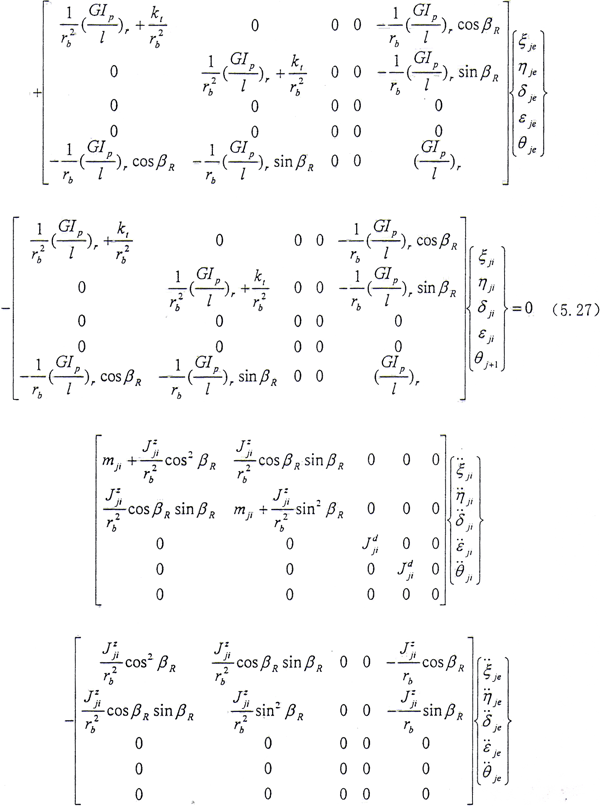
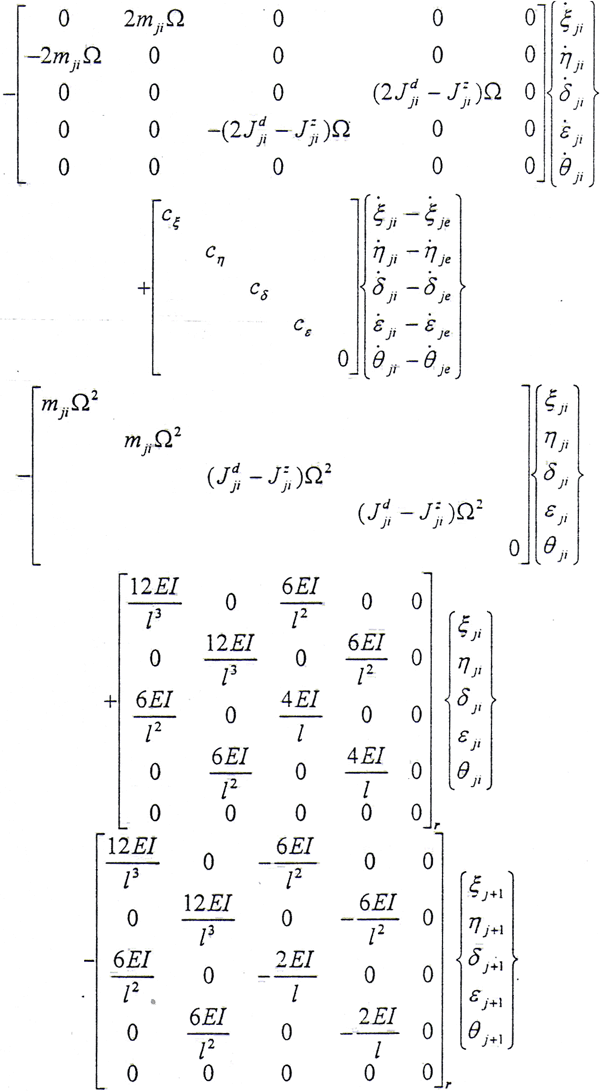
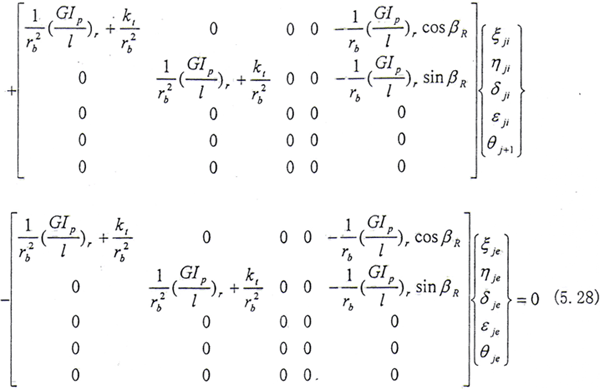
(5.27)式、(5.28)式中所定义的Ω方向与Z轴方向相同,当Ω方向与Z轴方向相反时,Ω以-Ω代入即可。从上式可见,方程系数矩阵中的元素与βE有关,而βR又与系统的广义坐标有关,因此方程是非线性的。只有在βR变化很小时才能进行线性分析。
通过上述过程,得到了半联轴器系统的运动微分方程,再与其他各结点的运动方程集合在一起,就得到转子—齿轮联轴器系统的运动方程。然而,对于旋转机械,在转子的某处总存在着轴承,即形成轴承—转子—齿轮联轴器系统,这样就需要引入支承条件,具体的做法是只要在转子—齿轮联轴器系统上具有轴承支承的自由度处用广义力(即轴承油膜力)来反映支承的影响。以滑动轴承为例,经过线性化处理后的油膜力在固定坐标系中可表示为
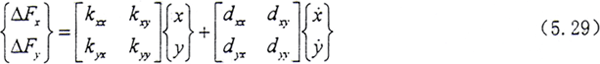
其中kxx,kxy,kyx,kyy为油膜刚度系数,dxx,dxy,dyx,dyy为油膜阻尼系数。
变换到旋转坐标系中以后
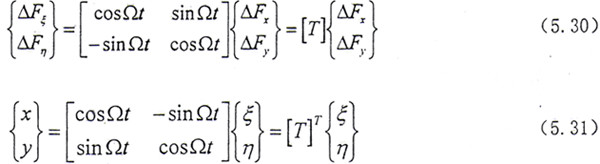
由此得

式中
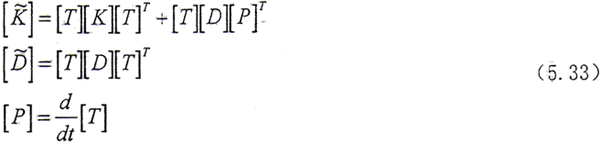
其中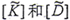 是与时间有关的(即其中的每个元素均是Ωt的正弦和余弦函数),只要将上面的
是与时间有关的(即其中的每个元素均是Ωt的正弦和余弦函数),只要将上面的 加到相应结点处的运动方程的左边,即可得到在旋转坐标系中的轴承—转子—齿轮联轴器系统的运动微分方程。
加到相应结点处的运动方程的左边,即可得到在旋转坐标系中的轴承—转子—齿轮联轴器系统的运动微分方程。
一个特例是当油膜刚度系数和阻尼系数采用如下关系
kxx=kyy=k kxy=kyx=0 dxx=dyy=d dxy=dyx=0 (5.34)
则得
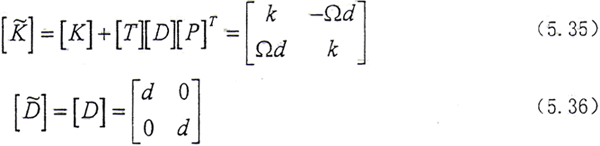
动态油膜力为
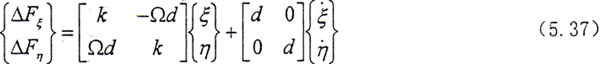
此时动态油膜力不随时间而变化。
如果在某些情况下,不能将滑动轴承的油膜力线性化或者因线性化而带来较大误差,那么可以采用非线性油膜力模型。
对于轴承—转子系统而言,弯曲振动和扭转振动是整个轴系振动的两个部分,以往在分析此类系统时往往把二者分割开来,原因是用来表征它们运动的广义坐标是解耦的,但在大型的轴承—转子系统中加入了齿轮联轴器之后,系统的弯曲振动和扭转振动就耦合起来了,不能再把二者分割开来。
这样集总后的轴承—转子—齿轮联轴器系统的运动方程。简写为

其中 {ζ}—系统的位移、转角列阵
[M]—广义质量矩阵
[C]—包括阻尼阵、陀螺力阵、科氏惯性力阵等
[K]—包括刚度阵、牵连惯星力阵等
以上在旋转坐标中建立了轴承—转子—齿轮联轴器系统的弯扭耦合运动微分方程,这样就可以深入地探讨联轴器内齿套和和外齿轮之间的相对运动关系以及齿轮联轴器在整体系统中的影响。
系统方程的无量纲化过程可参见第三章3.5节。
上一页
下一页


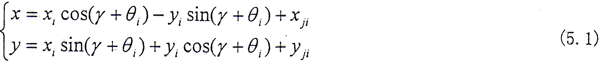
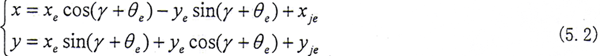

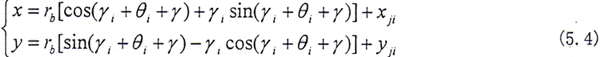
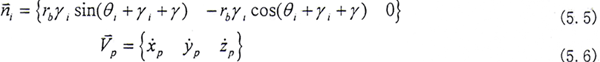
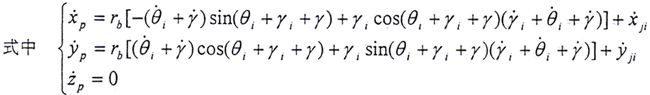
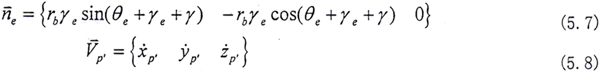
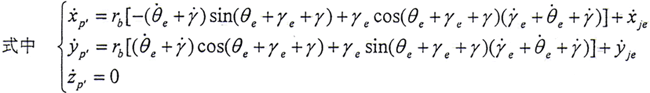
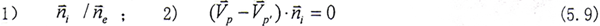
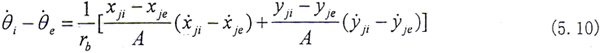
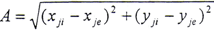


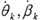 k=i,e是小量时,则
k=i,e是小量时,则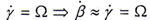 此时,β是以Ωt加上一个微小变化的转角。这样内齿套、外齿轮及二轴中心线的连线均是以轴的转动角速度Ω加上一个微小变化的量旋转的。
此时,β是以Ωt加上一个微小变化的转角。这样内齿套、外齿轮及二轴中心线的连线均是以轴的转动角速度Ω加上一个微小变化的量旋转的。

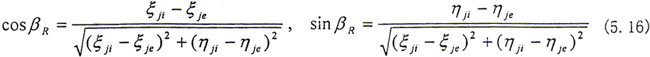
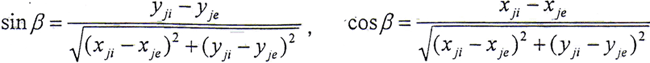
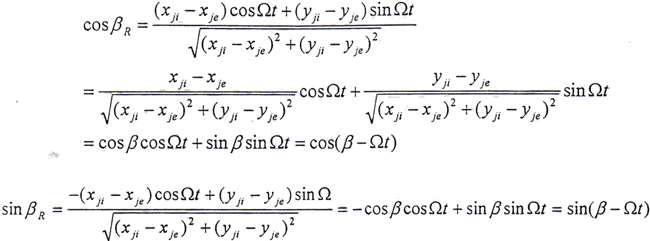
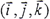 ,o1xmymzm系的单位矢量为
,o1xmymzm系的单位矢量为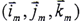 ,(m=1,2,3),则圆盘的转动由如下三个步骤完成:
,(m=1,2,3),则圆盘的转动由如下三个步骤完成:
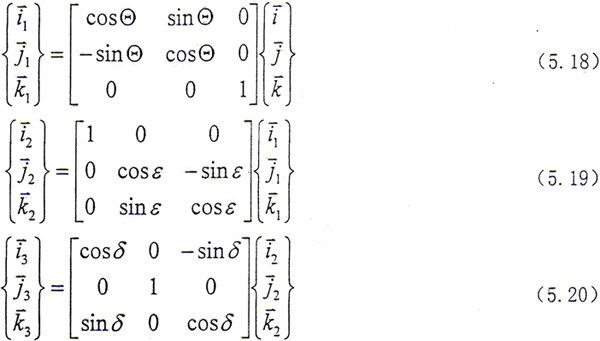
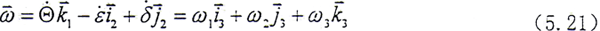
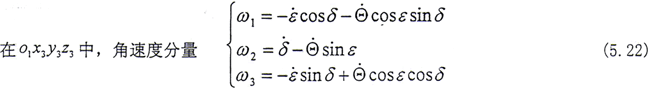

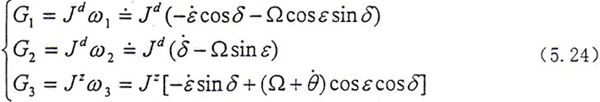

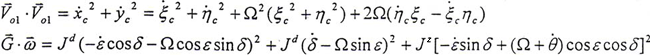




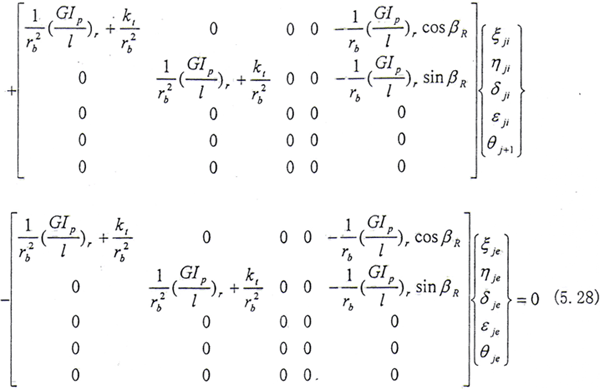
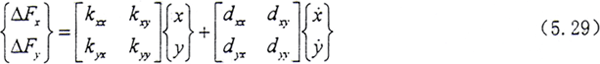
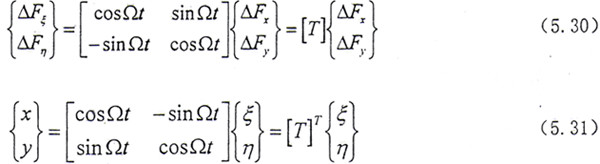

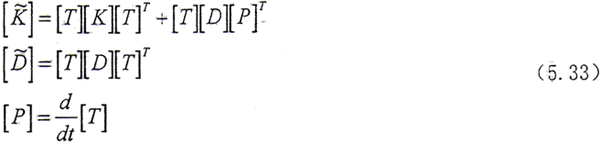
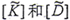 是与时间有关的(即其中的每个元素均是Ωt的正弦和余弦函数),只要将上面的
是与时间有关的(即其中的每个元素均是Ωt的正弦和余弦函数),只要将上面的 加到相应结点处的运动方程的左边,即可得到在旋转坐标系中的轴承—转子—齿轮联轴器系统的运动微分方程。
加到相应结点处的运动方程的左边,即可得到在旋转坐标系中的轴承—转子—齿轮联轴器系统的运动微分方程。