§2.3.2 齿间的间隙分布及啮合点轨迹
1 ).相对径向位移
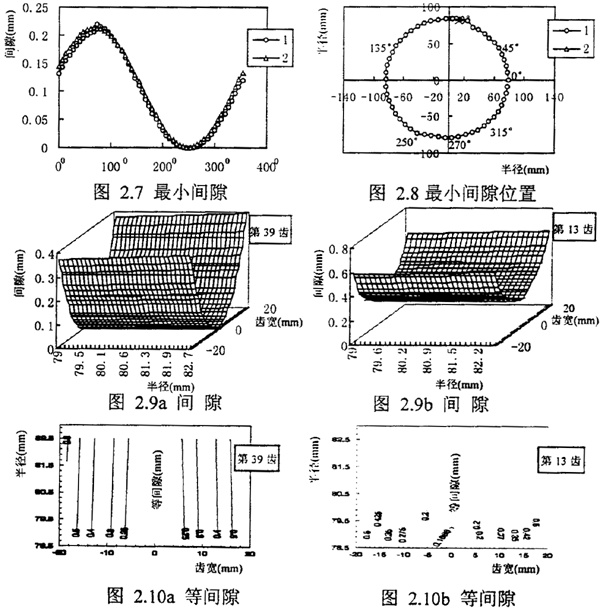
不失一般性设内齿轮为主动轮外齿轮相对内齿轮径向位移Δx=-0.2mm,Δy=0.无载荷的情况下计算结果:图2.7是内齿旋转一周时任意一对齿的最小间隙的变化或在任意的转角0下各齿对的最小间隙。2.8 图是半径方向最小间隙所在的位置,由于外齿是鼓形齿且没有偏角,在无载荷的情况下只在齿轮的中央齿廓处啮合所以仅画出半径方向最小间隙位置。图2.7 曲线1 是用本章方法计算的结果,曲线2 是用Heinz 几何方法计算的结果,我们可以看出用两种方法计算最小间隙的大小非常一致,但位置不同图2.8 ,因为Heinz 方法仅规定内外齿在分度圆上啮合,本文是从全齿高啮合状态来考虑最小间隙及其位置的。图2.7中250° 近间隙为零,即在无载荷或轻载荷时内外齿轮在此处附近的对齿啮合,相应图2.8 在250°啮合处的纵坐标大致为基圆的半径,即啮合线与基圆相切并与△x 位移线平行,这与前面所说与零齿差齿轮啮合相似;图2.9, 2.10 是在θ=0时第39 齿(图a)和第13齿(图b)的齿面间隙和等间隙曲线,从图中可以看出最小间隙在齿宽的中央,这是因内外齿没有发生相对转角位移,而且间隙沿齿高方向间隙变化的梯度小,即分度圆上的间隙与齿高方向的间隙相关很小,而沿着齿轮轴向的间隙变化的梯度较大,等间隙曲线沿轴向分布呈带状,这也是Heinz和本文计算最小间隙大小相近的原因。
2)相对转角位移
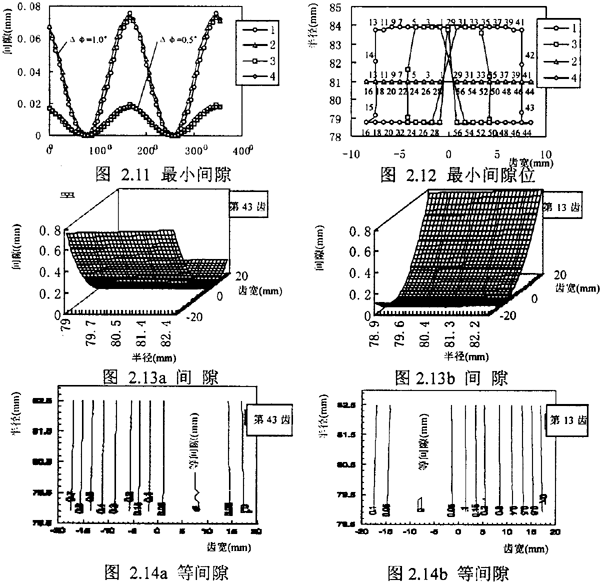
不失一般性设内外齿轮为主动轮,外齿轮相对内齿轮转角位移沿Y轴偏转为φ=1.0°或0.5°,沿X轴偏转为ψ=0.0。计算结果图2.11是内齿旋转一周时任意一对齿的最小间隙或内齿轮在任意的转角下各齿对的最小间隙,图上所示是φ=1.0°,0.5°两种情况,最小间隙近似为零的点在70°,250°两处附近这是由于齿轮联轴器的对称性所决定的。但两者的啮合位置不则,分列在齿宽中心的两则;图2.11图中曲线1、3是本章方法计算结果,曲线2、4是Heinz方法得到的结果,其其两者结果非常相似,但从啮合位置上看图2.12两都有区别,本文对齿轮联轴器啮合位置的计算是以全齿面为对象,进行三维分析,面Heinz则只规定在分度圆上啮合,本文计算齿面最小间隙位置大部分位于齿的边缘、齿顶、齿根,Heinz得到的最小间隙位置集中在分度圆上,即沿半径方向位置不同。但也有相同之处,即沿齿轮轴向位置很接近这丛7.12中可以看出,且分散范围随相对角φ值增加而增加。从齿面间隙图7.13和等间隙图7.14中观察,齿面等间隙曲线沿轴向分布呈带状且变化梯度较大,而间隙沿啮高的方向变化不大,这也是用两种方法计算最小间隙大小比较一致的原因。综合上面的结论我们可以推断,在齿轮联轴器传递载荷时,其主要的承载齿在最小间隙等于零附近,其啮合区域的形状近似为还状,其力的整个啮合区域内的分布也应为带状。从上面结论看几乎和径向位移得到结论相似。
3)相对转角位移和径向位移同时发生
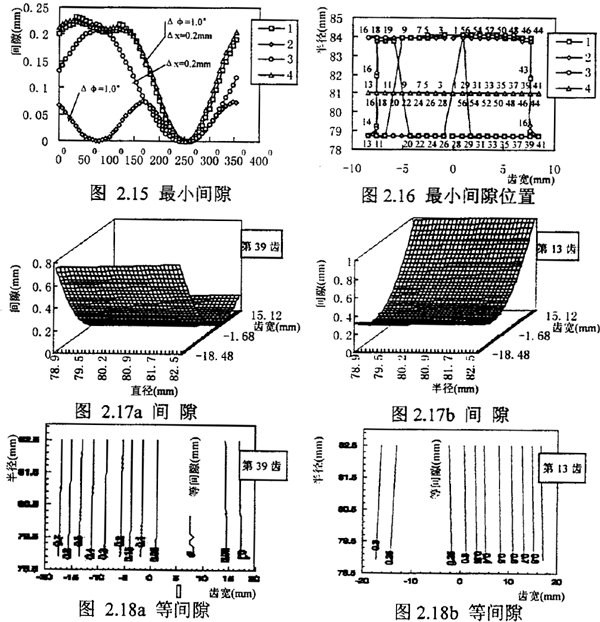
不失一般性设内外齿轮为主动轮,外齿轮相对内齿轮沿Y轴偏转角为,φ=1.0°,沿X 轴偏转为ψ=0.0,相对径向位移x=-0.2mm,y=0.0mm。相对转角位移和径向位移同时发生时,其最小间隙曲线.基本是前两种情况的叠加如图2.15~2.16 但又与以上的两种位移不同,其主要表现在啮合位置上和,其啮合位置不象径向位移那样在齿宽中央啮合而具有转角位移的分散特性,也不象转角位移那样最小间隙具有对称性(有相隔180°的两个齿对处间隙相近)。即综合位移即改变了纯转角位移齿轮联轴器最小间隙大小的对称性,使其最小间隙位置只有一处,又改变了纯径向位移最小间隙位置沿轴向的不变性。另外整个齿面间隙和等间隙(图2.17~2.18)的特点与前两者相同。
从啮合状态三种位移形式的分析来看,三者具有共同特点,既啮合齿对间隙沿轴向呈带状分布,且沿齿高方向变化梯度小,沿轴向变化梯度大。与Heinz 计算结果相比主要有以下异同点和优点:
1.两种方法计算最小间隙的大小非常相近,且最小间隙近似为零所在齿对基本相同,即用两种方法都可以估计联轴器传递扭矩时,主要由最小间隙近似为零处的几对齿承载,并能确定承载齿对的大致的方位和数目。
2.两种方法计算最小间隙的位置不同。
3.一般说齿轮联轴器的内外齿加工后还要边缘修形,但如何控制其修形量的大小关系到齿轮联轴器工作性能和寿命,而Heinz方法只提供估计受载的齿对大致的方位和数目方法,没有提供内外齿加工后边缘修形量的数据。本文计算结果反映了全齿面啮合状态,即可以提供估计受载的齿对大致的方位和数目方法,又可以作为内外齿加工后边缘修形量的数值参考。
§2.4 结论
本章主要对齿轮联轴器内外齿轮发生径向位移和转角位移时,内外齿面的三维啮合状态分析,主要得出以下结论:
1 ).最小啮合间隙及位置随着内外齿相对位移的变化而变化。
2 ).齿面间隙呈带状分布,且沿齿高的方向间隙变化的小,而在齿幅的方向上间隙变化的大.如果一对齿受载变形,其啮合区域的形状近似为带状,其齿面载荷也近似呈带状分布,且沿齿高的方向上力的剃度小,沿齿幅的方向上力的梯度大。
3 ).用本章计算方法得到的最小间隙与Heinz 计算结果几乎相同,并揭示其相同的原因。都可以提供估计受载的齿对大致的方位和数目方法。
4 ).本文计算的全齿面啮合间隙可作为内外齿加工后边缘修形量的数值参考。
上一页
下一页



