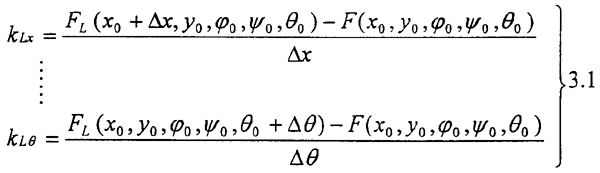第三章齿轮联轴器刚度分析及测试
§3.1简述
本章主要对齿轮联轴器本身的静动特性进行研究，由上一章齿轮联轴器啮合特点对齿轮联轴器力学模型进行简化，据此模型对齿轮联轴器进行了力学分析，推导静平衡方程，并在稳态情况下对刚度进行线性化处理；用数值的方法对其附加力、附加力矩和齿轮联轴器的刚度进行了计算。本章还推导了齿轮联轴器内外齿面相对速度公式，推导了齿面间存在干磨擦情况下的静平衡方程，计算了磨擦力对齿轮附加力，附加力矩的影响。为了验证理论推导，设计了试验装置，对鼓形齿及直齿联轴器附加力矩进行了试验和测试，与理论计算结果进行了比较。
§3.2齿轮联轴器刚度的定义
设齿轮联轴器的内外齿轮发生相对转角和径向位称（x0,y0,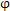
0,ψ0,θ0）时，附加到内外齿轮的力分别为Fx,Fy,F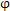,Fψ,Fθ其中FX，Fy为沿（x,y）轴方向的分力，F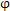,Fψ是绕（x,y）轴的弯矩，Fθ是扭矩，一般说Fx,Fy,F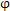,Fψ,Fθ是内外齿轮相对位移（x,y,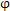, ψ, θ）的函数，既：FH（x,y,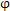, ψ, θ）其中H= x,y,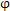, ψ, θ。其在静态平衡位置（x0,y0,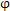0,ψ0,θ0）处齿轮联轴器刚度为：
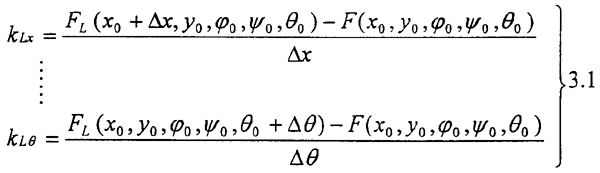
由此可以定义齿轮联轴器25个刚度系数。其写成矩阵形式为：
[KLH]5×5其中L，H= x,y,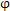, ψ, θ
其意义为：内外齿在平衡位置（x0,y0,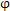0,ψ0,θ0）外，由于L方向的微小位移，在H方向上增加的力。L=H为主刚度，L≠H为叉刚度。
上面的定义方法类似于轴承动刚度的定义，即在某一个平衡位置（x0,y0,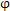0,ψ0,θ0）处定义齿轮联轴器刚度，从面齿轮联轴器刚度可简化成如图3.1所示的模型。从上面的分析可以看出，要求得齿轮联轴器的刚度，首先必须对内外齿轮进行受力分析，列出静平衡方程FH（x,y,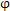, ψ, θ）。
§3.3 静平衡方程的前置预处理和基本假设
§3.3.1 齿轮联轴器模型与外齿轮模型的区别
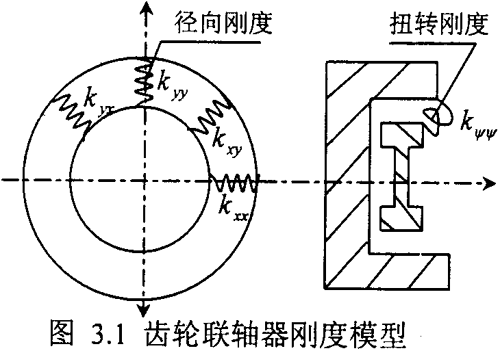
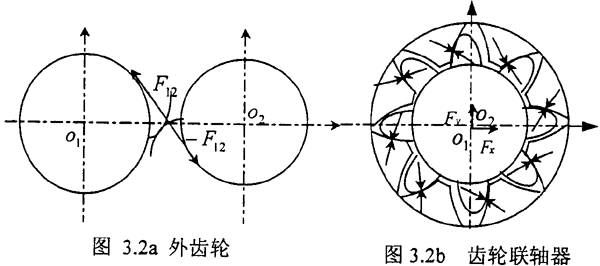
外齿轮啮合和齿轮联轴器内外齿啮合区别如图3.2a、3.2b。其外齿轮在传动过程中其啮俣线仅有一条且与两个外齿轮相内争，而齿轮联轴器内外齿啮合具有多齿接触的特点，它啮合线不只一条，其方向沿整个圆周方向并不一致。
§3.3 静平衡方程的前置预处理和基本假设
§3.3.1 齿轮联轴器模型与外齿轮模型的区别
外齿轮啮合和齿轮联轴器内外齿啮合区别如图3.2a、3.2b。其外齿轮在传动过程中其啮俣线仅有一条且与两个外齿轮相内争，而齿轮联轴器内外齿啮合具有多齿接触的特点，它啮合线不只一条，其方向沿整个圆周方向并不一致。
在以往对外齿轮模型简化时主要采用两种方法如图3.3a、3.3b几何模型和力学模型。在几何耦合模型中，齿轮轮齿被视为刚体。假定：1.啮合过程中轮齿始终保持接触，不脱啮。2.啮合线方向保持不变。要满足假设1，按两齿轮接触表面法向速度相等原则：
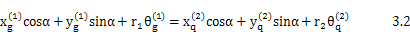
对式3.2两边积分可得到相应位移扰动关系：
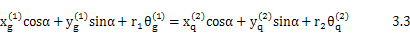
从而得到弯扭之间的关系式。
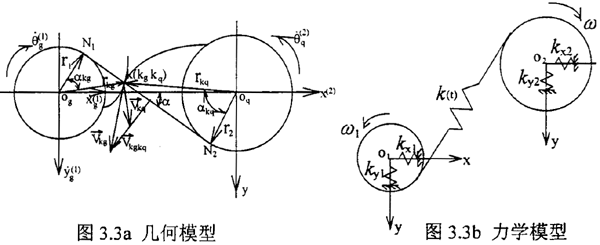
但这种模型假设不适合处理齿轮联轴器，因为采用这种刚体齿模型，当齿轮联轴器内外齿发生微小位移时，齿轮联轴器将从完全对中时的多齿接触状态，变为单齿接触，其附加力将发生突变，使我们将无法在线性范围内对其进行讨论，而且实际上由于齿的弹性，在内外齿轮发生相对位移时附加到齿轮联轴器的力并不是突然集中到某一个齿上，而是有一个变化的过程，因此我们应采用弹性齿模型。但它又不同于采用弹性齿的外齿轮力学模型，在外齿轮的力学模型中，将齿轮本体视为刚体，轮齿为弹性体，假定：1 、齿轮啮合过程中始终保持接触，不脱齿；2 、啮合线方向保持不变。轮齿刚度简化成沿啮合线方向的弹簧如图3.3b 所示，这是Lund 所采用的齿轮弯扭耦合模型，其位移协调关系如下：
( xl-x2)cosα+（y1-y2)sinα-r1θ1-r2θ2-(k1+k2)P=ε 3.4
其中α为啮合线与x 轴的夹角，r1、r2为齿轮基圆半径，x1、y1、x2、y2为横向位移，θ1、θ2为扭转角位移，k1、k2为二啮合齿沿啮合线方向的柔度，P为动态啮合力，ε为啮合误差。式3.4 的前提是齿轮啮合刚度不变，啮合过程中不脱齿，啮合线方向保持不变。
但齿轮联轴器则不同，由于其多齿接触的特点，不象外齿轮那样具有一条啮合线，而是有若干条啮合线，方向各不相同，且每个齿对所提供有效啮合刚度的大小和方向也不同，因此处理外齿轮方法并不适合齿轮联轴器。因此我们在对齿轮联轴器刚度模化时，要根据其多齿接触特点，选择一个固定参考坐标系，将整个圆周上的所有齿对有效啮合刚度（即该齿对接触部分的啮合刚度）折合到参考坐标系中，可以说齿轮联轴器刚度模化的实质是一折合刚度。其刚度的大小与齿轮联轴器内外齿轮原始相对位移（静态位置）有很大关系，因为在不同内外齿轮相对位移下，齿轮联轴器承载的齿数及接触位置将发生变化，每个齿对有效啮合刚度的大小和在整个圆周的分布位置也将发生变化，从而影响折合刚度大小。因此我们在处理齿轮联轴器模型时引入静态平衡位置的概念，在静平衡位置处对其刚度进行线性化处理，这是本文研究齿轮联轴器刚度的主要思路。
从上面分析可知由于齿轮联轴器内外齿啮合的复杂性，使得对模型的处理要比处理外齿轮啮合复杂的多。我们必须弄清齿轮联轴器对的接触状态以及载荷分布特点，以便建立合理的力学模型。第二章已经对接触状态进行分析，下面对齿的载荷分布进行讨论。
§3.3.2 齿面载荷分布及齿轮联轴器力学模型建立
目前对齿轮的载荷分布问题的理论研究大致可以归纳为以下4 种：
1 ．按ISO观点对载荷的分布，假定载荷均匀分布于齿的接触线上，由此求得由于支承系统和齿轮的变形所引起的载荷分布不均。
2 ．根据支承变形和齿轮变形的平衡条件建立微分方程用数值方法求解。
3 ．假定某种载荷的分布，用迭代的方法求解。
4 ．由两接触物体间接触区离散点的变形，以线性规划的单纯形法为工具，用数值分析的方法，求解齿轮的载荷分布。
这些方法繁简不同，优劣个具，其中应用广泛，考虑影响因素较为系统全面，但却较复杂，其中忽略了材料的连续性和齿端面柔度较大因素的影响，将使计算结果是近似的。另外三种方法都是随着计算机的广泛应用而提出的较为精确的数值计算方法，使问题的解决更符合实际情况。
计算齿轮联轴器的载荷分布理论模型很多：中岛Is ］等人把齿轮联轴器每个啮合齿对模化为一个弹簧，而忽略因为内外齿端面接触造成内外齿啮合刚度下降的影响；文献181 为了考虑齿轮本身周节误差对载荷分布的影响，把齿轮联轴器内外齿作为两个矩形齿齿条处理，其实质也是将内外齿模化成一个弹簧：其上述两种方法的优点是模型简单，可以较方便估计出齿轮联轴器的主要承载齿对，但此方法不能计算每一对齿的载荷分布，且把每一对齿的刚度看成是不变的，即忽略齿对接触面积不同其刚度变化的因素，因此这种方法过于简单，对于齿轮联轴器整体刚度的计算影响很大。日本的土居良规等人［' 41 在齿轮花键轴齿面载荷分布的计算中，把齿轮进行了片状离散化处理；王秀琦［6l 等人把整个接触齿面离散成若干个点；这两种模型共同的特点是把内外齿看成是若干刚度相等弹簧组成，同时忽略了材料的连续性，从而初步讨论了载荷沿齿面方向的分布；但这两种方法都没有计入齿轮啮合刚度的边缘效应。
对于鼓形齿联轴器来说，由于外齿轮是鼓形，内齿轮的啮合状态比较复杂，齿面的接触状态及载荷分布也比较复杂，我们不可能得到齿面载荷的准确分布，只能对其进行近似的拟和。根据第二章的结论可知，在无载荷的状态下,鼓形齿联轴器内外齿齿面的等间隙图曲线沿齿轮的轴向呈带状分布，沿齿高方向的间隙的变化梯度很小，其齿高方向间隙可以用相应分度圆上的间隙来代替。由此我们可以推断，由于载荷的作用，齿发生弹性变形，如果某一对齿受载相互接触，其首先在最小间隙附近齿对接触，而且齿面接触区域的形状近似呈带状，其力在整个接触区域内的分布也近似为带状分布且沿齿高的方向上力的梯度小，可以看成是均匀分布，沿齿幅的方向上力的梯度大。为了对该载荷分布进行很好的拟合，参考ISO 对载荷的分布的处理方法以及上面所提到对齿联轴器载荷分布的第二种模型，再结合第二章的结论，我们把鼓形齿联轴器内外齿沿齿向离散成若干微元。本文对其齿对模化的特点是计及了齿轮联轴器啮合刚度的边缘效应（内外齿端面接触时啮合刚度较小）和鼓形量等因素，具体模化方法和基本假设如下：
把轮齿沿齿轮的轴向进行离散化，将其分割成M 微元，每一微元的宽度为bj，其中bj＝B / M , B 是齿的宽度，当分割微元的宽度很小时，其该微元齿面载荷的分布近似均匀，把齿面沿齿高方向的分布力等效到分度圆上为了简化计算我们作以下假设：
1 ．假设外齿第j个微元在与内齿接触变形时，其变形量等效到分度圆轮廓的法向处理。
2 ．把每一个微元啮合齿对看作是相互独立互不影响的弹簧，忽略了材料的连续性，其方向沿分度圆外轮廓的法向。
3 ．齿的误差、变形以及原始间隙都等效到分度圆上处理。
由上面简化可以得到每齿对简化的力学模型：如图3.4 。所以我们可以用第j 个微元第i 个齿廓法向啮合刚度kj与第j 微元第i 个齿对内外齿沿分度圆齿廓法向相对变形δji,的乘积，即fji=kjδji来表示第j分微元第i个齿分度圆上受到的等效力fji。则用此数值方法可以方便计算出每个齿的载荷分布，其中fi=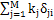
,fi为载荷分配到第i个齿的分额。fji在j=1，2，3……M时表示第i个齿齿面沿轴向的分布，从而计算出整个齿轮联轴器的受力情况。具体的计算由下节给出。
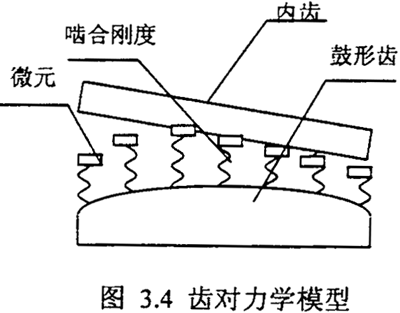
此方法的优点：
1.可以记入齿轮沿齿向鼓形量和误差。
2.与ISO模型和模型相比本文记入轮齿啮合刚度在齿的边缘较小因素的影响，引入刚度沿齿面分布系数（具体由下节计算）。
3.可以运用数值方法对联轴器的附加力和力矩及齿轮联轴器折合刚度进行求解。
本章所涉及的几个坐标：
1）O—XYZ：是固定坐标系，O是内外齿轮对中时内外齿轮中心Z是齿轮联轴器的轴向。
2）OK-XKYKZK：分别代表固定在内外齿轮上的坐标，OK是内外齿轮中心（k=N，w表示内外齿轮）。
3）
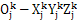:表示固结在第j个分割微无上的坐标，
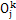是轴向第j个分割微元的中心（k=N,w表示内外齿轮j=1,2……M）。
4）
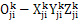:是固结在第j分割微元第i个齿上的旋转坐标，
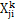坐标是分度圆齿廓切线方向，
是齿廓法向方向，
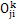是轴向第j个分割微元的中心（k=N,w表示内外齿轮j=1,2……Nz）。
§3.4 齿轮联轴器静平衡方程
§3.4.1 齿对啮合刚度及分布系数
由前面的处理和假设分布力等效到分度圆上，则单齿对啮合刚度也是在分度圆上定义的，其定义如下：
使一对啮合齿对在单位齿宽上、沿分度圆法向上、产生平均单位挠度所施加在分度圆齿廓法线方向的等效载荷。
具体计算时一般把单位齿宽上施加均匀的分布力等效到分度圆上、计算出单位齿宽的沿分度圆齿廓法线方向平均位移。设f 是施加在单位齿宽分度圆法向上的分布力，δ产生的平均位移，则该处单位齿齿宽的刚度为：
k=f/δ 3.5
因为在同一位置不同的载荷下有不同的刚度值，一般我们取几个刚度的平均值。另外在齿的轴向不同的位置接触时，齿所表现的刚度也不同，一般齿宽中央的刚度大而到两端的刚度小，我们引入刚度系数ks，ks代表在齿宽不同的位置的单位齿宽的刚度与齿宽中央单位齿宽刚度的比值，是一个相对值，我们可以在齿宽方向上拟合出一条（ks---Bj）曲线。其中：Bj是齿宽方向的位置，ks=kj/k0,下一节我们用有限元法计算此值。
为了计及齿轮的边缘效应，即一对齿在边缘接触时其啮合刚度有下降的特性。我们采用弹性体三维有限无数值计算。
2）齿轮有限元网格和边界的划分
用有限无法计算齿轮的变形和应力的应用程序很多，理论也非常成熟，有专门有限元通用软件。影响计算结果的主要原因有：边界范围的选择，单元形式的选择。为了减少计算是境和对计算机容量的要求，通常取一个齿轮为计算模型。
1）边界范围的选择
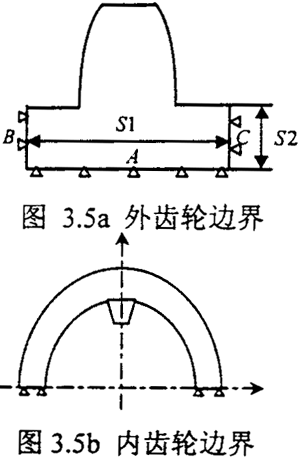
对于外齿轮Daimler-Benz公司选取边界的方法是先取半个齿轮进行有限无计算，这是从整体来考虑问题，然后根据计算的结果来选择边界的范围，其所定的边界宽度如图3.5a，S1=6.1m，m是齿轮的模数。Chaber所取的边界的方法是考虑圣维需原理，其所定的边界深度为S2=1.5m。综合以上两者的研究，用有限无计算外齿的变形，计算模型的边界范围可取：
S1≥6.1m ,S2≥1.5m
其内齿的边界范围如果齿圈的厚度很薄时为了记及齿圈的变形取半个齿轮，如图3.5b所示：
2）边界上各节点的约速条件
边界上各节点的约速条件对计算结果影响也很大，具体的约速条件与齿轮的结构有关，一般有：给定边界节点的位移，给定边界节点的载荷，自由边界点。本计算中所选择的边界条件如图3.5a所示，底面A侧面B、C选择为固定边界其他面的边界节点为自由边界。内齿轮选择的边界条件如图3.5b所示
3）网格的划分和单无类型的选择
鼓形齿和内齿的网格划分，采用8节点的三维实体模型
4）节点载荷
根据上一章的结论齿宽方向间隙呈带状分布，在齿高方向变化梯度小我们可以推断出在齿对受载变形时，其接触区域的形状也近似呈带状分布，且沿齿高方向接触区域力的分布近似均匀，如果网格在轴向分割宽度很小时则力的分布近似为均匀。其把齿面的分布载荷等效到各个节点上载荷。
5）位称和刚度分布系数计算
假设沿轴向将齿分割成M微元，每一分割微元宽度为bj包括个节点，通过三维弹性实体有限元程度计算出在分度圆上节点沿齿廓法线方向上的位移为δi，i=1，2，3，……L，则分度圆平均位移为：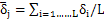
,设等效到分度圆上的分布力为fj（单位Kg/mm），所以在bj处单位宽度所求得的等效刚度为：k
j=fj/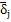
。设齿中央处等效刚度为ko，对kj值进行无量纲化即可以得到沿齿宽方向刚度分布系数ksj。
计算实例，联轴器内外尺参数：模数2.0mm；齿数：20齿；内外齿宽分别为：15mm、15；压力角为：20°:鼓形量为：96；内齿圈外径：60mm。分割成10个微元，则外齿轮内齿轮沿齿宽方向的刚度分布图3.6a、3.6b。纵坐标为刚度分布系数，其无量纲参数选则三种载荷下外齿中央处等效刚度的平均值：k0=1920kg/mm2(曲线1是fj=1.2kg/mm、2是fj=1.0kg/mm、3是fj=0.8kg/mm),横坐标是齿宽无量纲值（元量纲参数为齿宽一半），内外齿边缘的刚度比齿宽中央刚度概小20%，内外齿边缘接触时啮合刚度要比齿宽中央啮合刚度来得小。
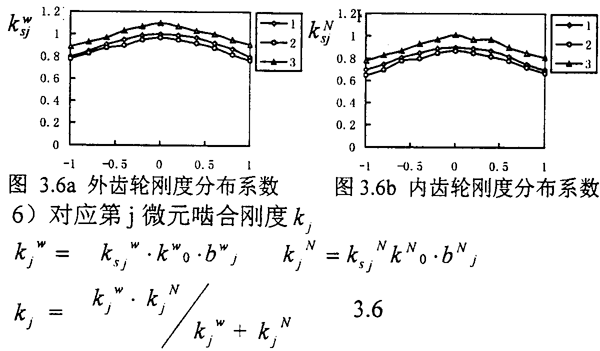
kjW,kjN分别表示内外齿轮对应第j微元的刚度，bwj=bNj 是分割微元的宽度；
k
sjw,k
sjN是齿轮中央处单位齿宽刚度的平均值，j=1,2,3……M。
上一页
下一页
