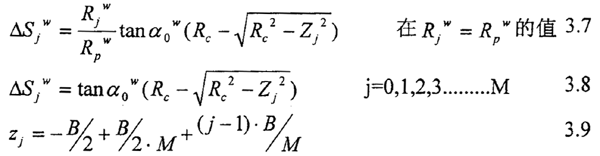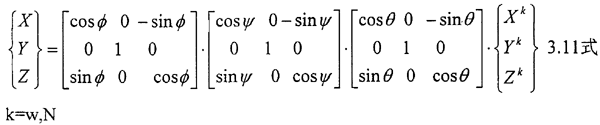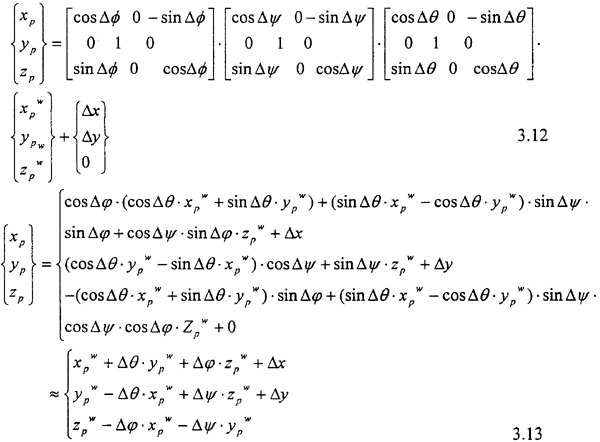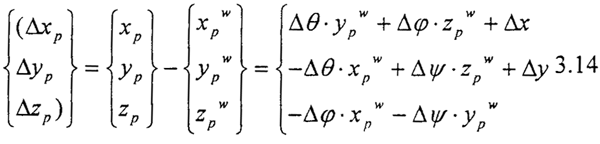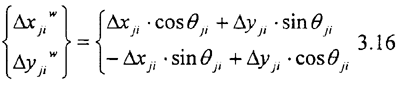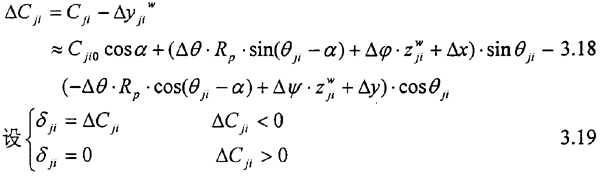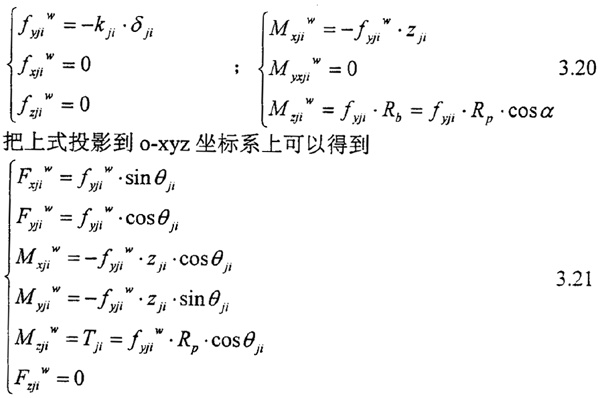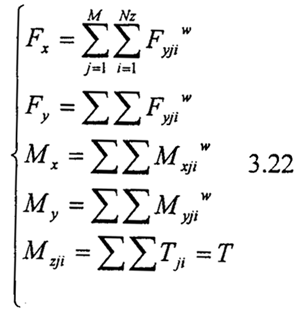§3.4.2  齿面原始间隙

由假设可知，齿面间隙、齿的误差以及内外齿的相对位移可以简化到分度圆上进行处理，既齿的相对变形等效到分度圆上进行处理，这样会对计算大大简化，齿对间分度圆方向的间隙可以由以下几项组成：

1．不考虑齿面误差时的分度圆上侧隙用C₀来表示，沿轴向对应每个分割的原始的侧隙都相等这由内外齿加工时的变位系数来决定。在传递扭矩时此间隙自动消除，因此对齿对之间的弹簧的压缩量不起作用。

2．由鼓形齿鼓形齿量所引起的分度圆上平均间隙用C_gj来表示，j=1,2,3……M，C_gj在分割微元宽度很小时近似等于第j分割微元齿宽中点的间隙，由第二章2.4式得：

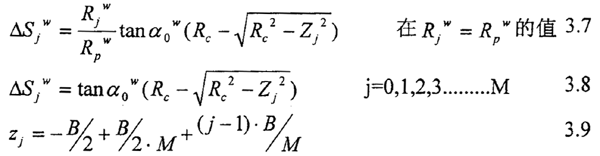
3．由于内外齿第i个齿的周节误差和其它齿形误差所引起分度圆方向的间隙C_pji,在分割微元宽度很小时C_pji近似等于第i个齿第j分割微元宽中点误差引起分度圆方向的间隙，一般在处理时认为内外齿没有周节误差和其它齿形误差。

综合上面引起分度圆方向的间隙的因素，可以得到第j分割微元第i个齿分度圆方向的平均间隙C_ji0:

C_ji0=C_gj+C_pji                                                      3.10

§3.4.3  内外齿轮相对位移引起间隙变化

如图3.7所示，O-XYZ；是固定坐标系，O是内外齿轮对中时内外齿轮中心Z是齿传输线联轴器的轴向，O^K-X^KY^KZ^K：分别代表固定在内外齿轮上的坐标，O^K是内外齿轮中心（k=N,w）表示内处齿轮），

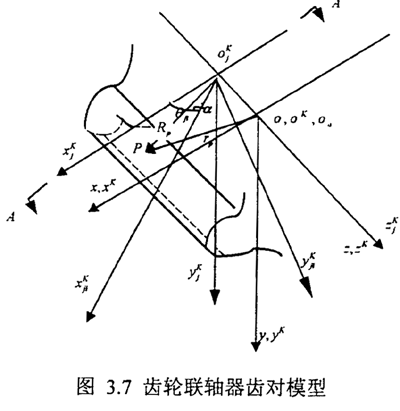
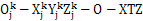的换矩阵为：

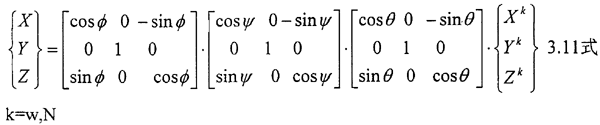
不失一般性设内齿轮静止即O^N-X^NY^NZ^N与静止坐标系数O-XYZ重合，以后用O-XYZ来表示内齿轮坐标，外齿轮相对内齿轮发生位移，位移量为：（Δx,Δy,Δ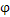,Δψ,Δθ）；Δx,Δy,Δ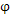,Δψ,Δθ为微小位移，则外齿轮任意一点P^W（X_P^W，Y_P^W，Z_P^W）在外齿轮相对内齿轮发生位移后，在静止坐标系内的坐标为：P^W（X^P，Y^P，Z^P）其值由式3.12～3.13定。

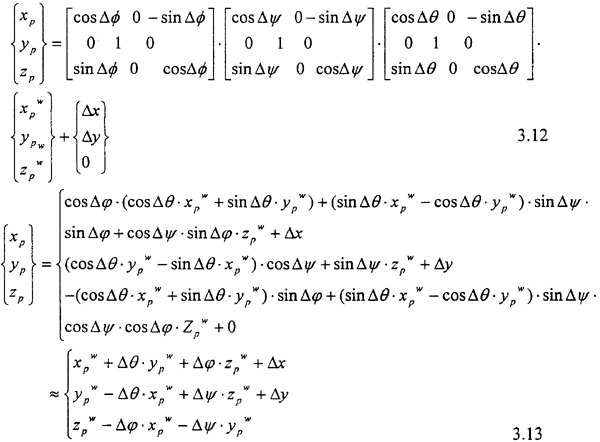
在外齿轮相对内齿轮发生位移前P点在O-XYZ坐标系中的坐标为：P₀（X_P^W，Y_P^W，Z_P^W），则P相对静止坐标系（即内齿轮）沿x,y,z方向的位移为：

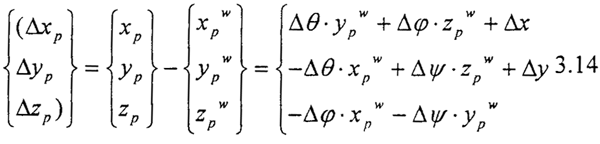
§3.4.4  静平衡方程的建立

如果按照前面的处理方法将处齿轮（鼓形齿）沿齿宽的方向分割成M个微元，则第j分割微元第i个齿上分度圆上相对内齿的平均位移（Δx_ji, Δy_ji, Δz_ji）可以通过式3.14 得到：

由第二章讨论可知，内齿轮一般不进行鼓形修形，其分度圆柱面上截得在轴向的齿形为直线，鼓形齿截得的形状为弧线，如图3.8所示：从图中我们可以看出外齿相对内齿的轴向位移，并不影响内外齿面的间隙，既不对齿的压缩变形起作用。因此我们取出图3.7中垂直齿轮轴线的A-A截面来讨论如图3.9，即对齿轮第j分割微元宽度中部截面。其中O_j^w-X_j^wY_j^w:表示固结在外齿第j个分割微元上的坐标，O_j^w是轴向第j个分割微元的中心，O_ji^w-X_ji^wY_ji^w:是固定在外齿第j分割微元第i个齿上的旋转坐标，X_ji^w坐标是分度圆齿廓切线方向，Y_ji^w是齿廓法向方向，O_ji^w是轴向第j个分割微元的中心，O_j^N-X_j^NY_j^N:表示与外齿第j分割微元对应的固结在内齿相应分割微元上的坐标，O_j^N是分割微元的中心，因为假设内齿轮固定所以O_j^N-X_j^NY_j^N与O_j-X_jY_j重合；O_ji^N-X_ji^NY_ji^N:是固结在分割微元第i个齿上的旋转坐标j=1,2……M，i=1,2……Nz。

第i个齿上的旋转坐标坐标轴X_ji^w是分度圆齿廓切线方向，Y_ji^w是齿廓法向方向，O_ji^w是轴向第j个分割微元的中心，O_j^N-X_j^NY_j^N表示与外齿第j分割微元对应的固结在内齿相应分割微元上的坐标，O_j^N是分割微元的中心，因为假设内齿轮固定，所以O_j^N-X_j^NY_j^N与O_j-X_jY_j重合，O_ji^N-X_ji^NY_ji^N:是固结在分割微元第i个的旋转坐标j=1,2……M，i=1,2……Nz。将Δx_ji, Δy_ji投影响到O_ji^w-X_ji^wY_ji^w坐标中：

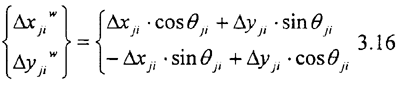
其中ΔY_ji^w为外齿轮第j分割微元第i个齿分度圆齿廓法线相对内齿的位移，ΔX _ji^w为切向位移，由于前面的假设中把内外齿看成是沿分度圆齿廓法线方向串防的弹簧，因此只有y方向的位移对弹簧起到压缩作用，而x方向的相对位移对弹簧起到压缩是高阶小量，可以忽略。

又因为在无载荷时内齿轮在分度圆周向的原始间隙为C_ji0-，周向与法向间隙的关系为：

C_ji=C_ji0·cosα                                    3.17

所以内外齿轮相对应的第j分割微元第i个齿分度圆齿廓法向间隙的变动量为：

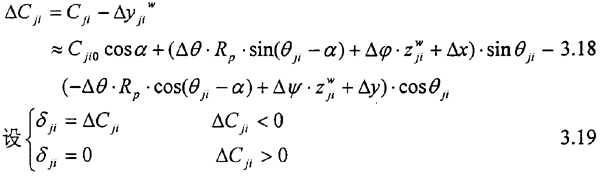
上式ΔC_ji--＜0说明内外齿发生相对位移后，齿面相对间隙为负，即内外对应齿对在j微元第i齿对处相互接触，δ_ji可近似的看作内外齿在j微元第i齿对处的相对变形。ΔC_ji--＞0说明内睁生相对位称后，齿面相对间隙为正，内外对应齿对在j,I处存在间隙，则可以认为内外齿在ji处的相对变形δ_ji=0。
则外齿轮第j分割微无的第i齿所受到的力和对于齿轮中心的力矩为：

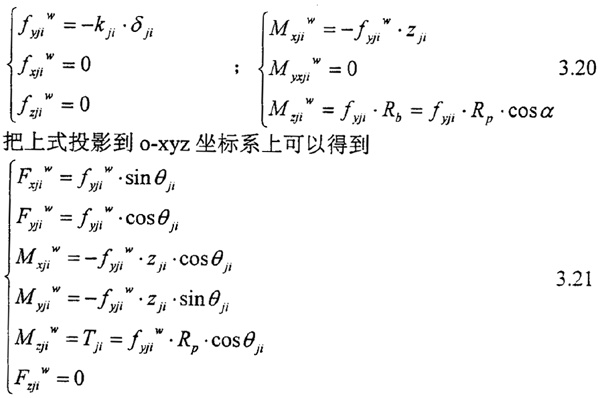
此式既为第j分割微元第i个齿对整个联轴器受力方程；那么所有的分割微元和所有的齿受力的叠加后，即可得到齿轮联轴器静平衡方程。

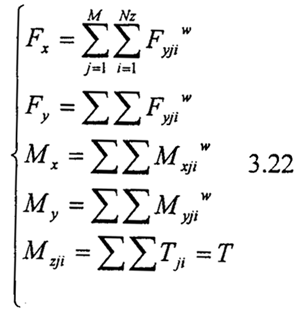
§3.4.5  无量纲化

为了计算方便，我们对上式进行无量纲化

上一页

下一页