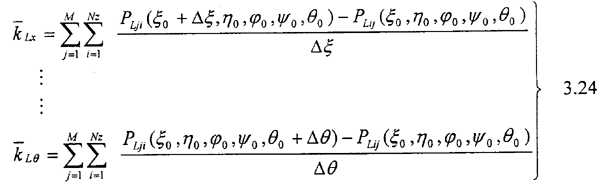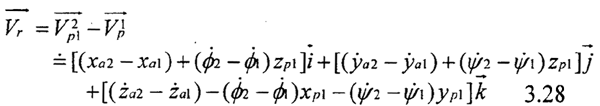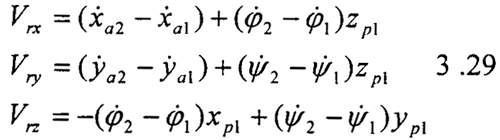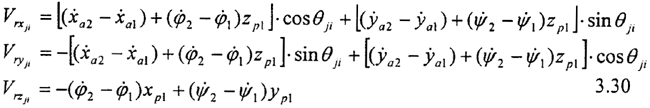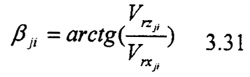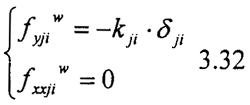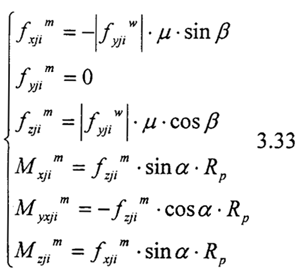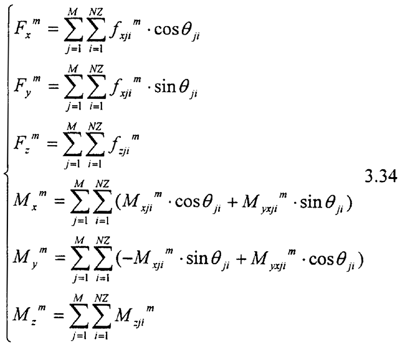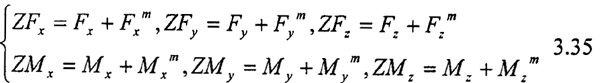§3.4.6齿轮联轴器刚度
多齿轮联轴器由于其齿接触的特点，不象外齿轮那样具有一条啮合线，而且啮合线的方向不同，所以在处理齿轮联轴器的模型时，需要选择一个固定参考坐标系，根据其内外齿的接触状态，将整个圆周上的所有齿对有效啮合刚度（即该齿对接触部分的啮合刚度）折合到参考坐标系中。因此齿轮联轴器刚度模化的实质是一种折合刚度。这种折合刚度的大小与齿轮联轴器内外齿轮原始相对位移（静态位置）有很大关系，因为在一同内外齿轮相对位移，齿轮联轴器承载的齿数及接触位置将发生变化，齿对啮合刚度和在整个圆周的分布位置也将发生变化，从而影响折合刚度大小。因此我们在处理齿轮联轴器模型时引入静态平衡位置的概念，在静平衡位置ξ0,η0,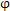
0,ψ0,θ0处对其刚度进行线性化处理。
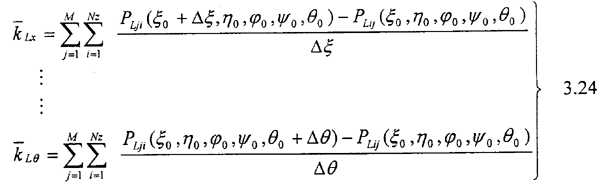
由此可以得到齿轮联轴器25个无量纲刚度系数，写成矩阵形式为：
[
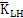]5×5-其中L，H=ξ,η,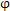,ψ,θ
在计算的过程中都是在一定的工况下进行的，即齿轮联轴器所传递的扭矩已知为T，在此工况下如果因某种原因使内外齿轮产生相对位移（ξ0,η0,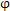0,ψ0,θ0）时，附加给齿轮联轴器的力为Pξ,Pη,P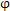,Pψ,θ0。因为θ0不能用显式表示出来，所以计算时要通过迭代来示到，具体过程如下：
已知在某一个条件下产生位移ξ0,η0,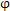0,ψ0,假设使联轴器产生的相对扭转角位移θ0，根据式3.23计算T，计算的T与给定的工况即联轴器传递的扭矩T相比较，当差值达到精度要求时，求出此时内外齿的静态力，反过来也就是在Pξ,Pη,P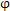,Pψ,T的工况作用下联轴器的静态位置为（ξ0,η0,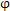0,ψ0,θ0）。如果没有达到精度则修改θ0值重复以上计算。得到静平衡位置后再利用式3.24求得25个刚度系数。
§3.5 考虑磨擦力齿轮联轴器附加力和力矩
§3.5.1 基本假设
1）设磨擦力为库仑磨擦力，磨擦力的大小与压力成正比，方向与相对速度方向相反。
2）设内外齿间相对分割微元之间的磨擦系数相等，设为μ。
3）相对速度发生在齿长方向。
§3.5.2 分度圆上内外齿相对速度：
图3.10是，齿轮联轴器第i个齿对的模型，设内齿套中心为oa1，相对定坐标为o-xyz的速度为：
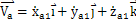3.25
相对坐标系oaξ1η1ζ1在oa点与联轴器固接，坐标系oaξ1η1ζ1以角速度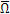
绕平移坐标系oa-x1y1z1旋转
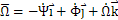,则位于相对坐标系任一点P（ξ1η1ζ1）处的绝对速度为：
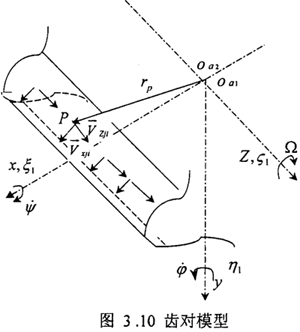
如P为啮合点，则在该啮合点上，P’点相对于P点的运动速度为：
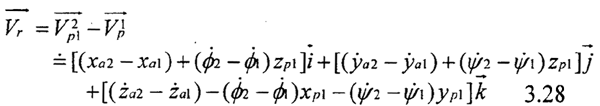
又
轴向窜动
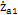=0，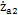
=0外齿套相对内齿圈的径向和轴向滑动速度为。
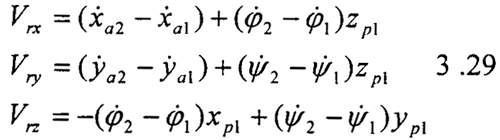
xp1,yp1为x1y1z1坐标系中的局部坐标，因此只要1，2的角位移振动不相等，则总存在有轴向与径向滑动，从而引起磨擦力和相应的力矩，如果把齿面间的磨擦看成是库仑磨擦，则第j 分割微元第I个齿分度圆上的相对速度，在固接在第j微元第I个齿上的局部坐标系oji-xjiyjizji上的投影为：
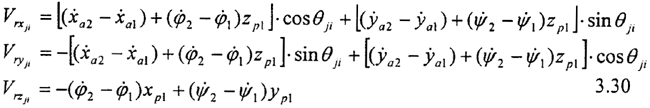
其中：xp1=RP·cos(θji-α) yp1= RP·sin(θji-α) zp1=zjiw
因为Vryji为齿面间的法向速度所以与磨擦力无关。
所以第j微元第I个齿对磨擦力的方向为：
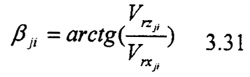
§3.5.3 考虑磨擦力齿轮联轴器附加力和力矩方程
由§3.4 分析得出齿面的压力为：
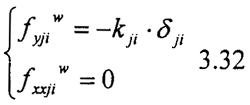
则第j分割微元第I齿所受磨擦力和对于齿轮中心的磨擦力矩为：
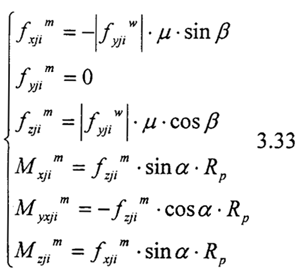
把上式投影到o-xyz坐标系并把所有齿和分割微元求和可以得到齿轮联轴器内外齿所受磨擦力和磨擦力矩：
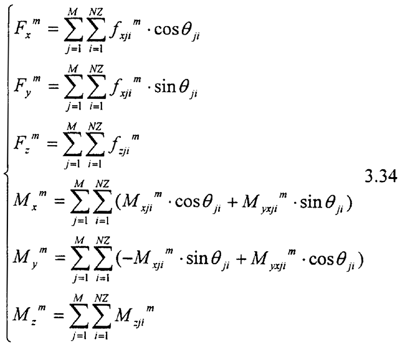
上式即为磨擦力方程。
上式+式3.22即得到总平衡方程：
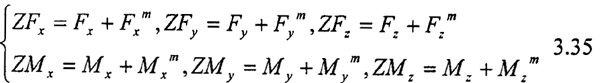
为了计算方便，我们对上式进行无量纲化
从上面的方程可以看出考虑磨擦力时，如果内外齿有径向不对中则有可能产生轴向力。第二章接触分析可知，这是因为有径向不对中破坏了齿轮联轴器接触的对称性。
§3.6 计算实例
§3.6.1 齿轮联轴器参数
模数：2.0mm，齿数：20齿，内外齿宽分别为：15mm，15mm，压力角为：20度，鼓形量为：96mm，我们选择三种工况（扭矩）进行测试（T1=3.07Kg·m，T2=5.50 Kg·m,T3=8.50 Kg·m）,取磨擦系数为μ=1.0，速度方向可以根据试验具体情况来模拟。不失一般性我们设内齿轮固定，外齿轮绕x轴的相对内齿轮的转角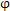为变量。
上一页
下一页
