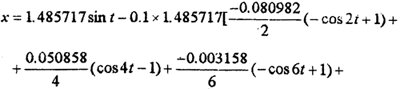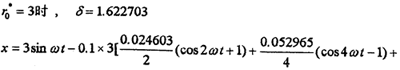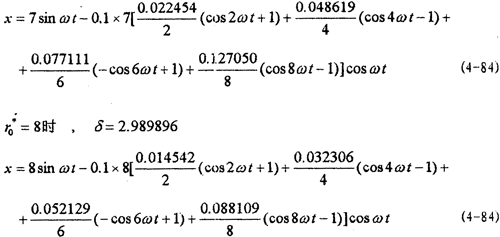4-3 近似解析解与数值仿真解的结果比较
为了说明柴油机闪—谐波平衡法的正确性和精度，我们分别用一个简单例子和大挠度弹性联轴器系统（4-2）进行计算，同时与相应的数值仿真计算作比较。
例 
+3x-3x3+x5-2x7+x9=0.1（-2.03059
+3cost） （4-76）
解析解为：
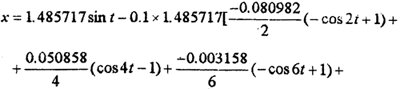
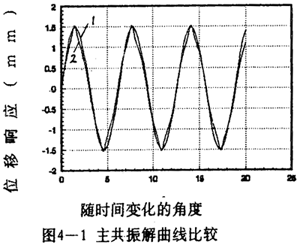
曲线图如图4-1所示。从图中可以看到解析解曲线1和数字仿真解曲线2重合性较好，在振幅与相位上误差都较小。
钢丝绳弹性联轴器系统（4-2）式中的参数取为：
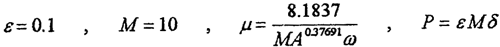
式中p为激励力幅值。
分别计算了八种振幅下的解析解和对应的数字仿真，如图4-2～4-9所示。曲线1为解析解，曲线2为数字仿真解。各对应的解析解为：
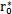=1时，δ=0.81837
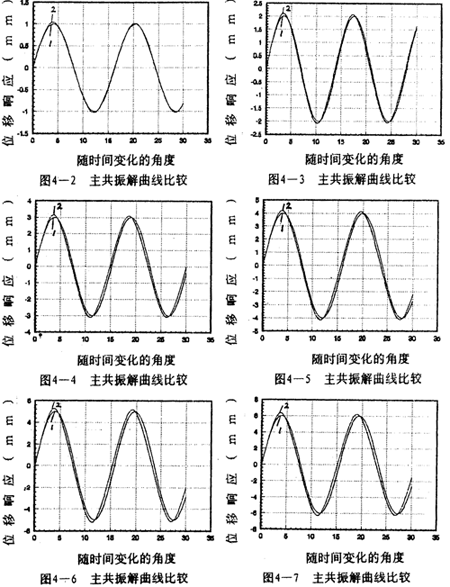
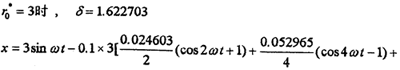
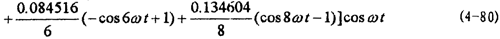
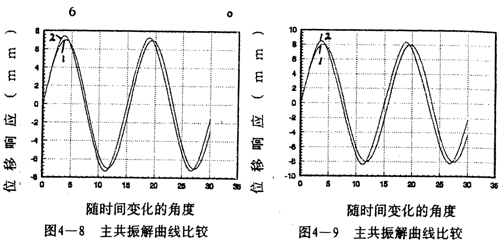
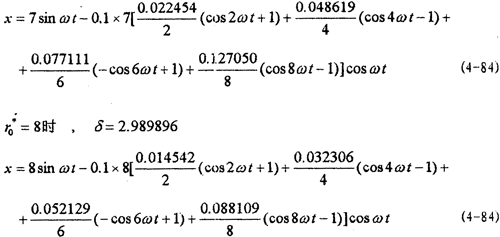
从各曲线图可以看到（1).解析解曲线1与数字仿真解曲线2的振幅误差较小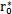，=1和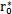=2时两者的重合性很好。(2).随着振幅的增大，解析解曲线1和仿真解曲线2在相位上产生微小变化，解析解的相位超前仿真一个小量，原因是随着振幅的增大，系统呈现更为强烈的非线性，而在推导中略去了高次项，但还是可以满足工程的要求。（3）从（4-78）-（4-85）式中的各δ值可知，在联轴器产生主共振的情况下，激振力很小。
4-4 小结
本章针对稳态响应求解问题，作了以下工作并得结论：
1.在研究前人求解非线性系统响应的基础上，针对稳态响应求解的买际需要，分析了方法的优点和不足，提出一种新方法—频闪—谐波平衡法，用于求解一类强非线性系统稳态响应的近似解析解。
2.频闪—谐波平衡法的优点是：从有关公式可以一目了然知道系统的基本参数对系统特性的影响，如由（4-16）式可以知道系统的固有频率p是动刚度、振幅、系统质量的函数，改变这些基本参数，可以改变系统特性，因此用这一方法对具有强非线性特性系统的动力学设计是十分有利的。
3.利用频闪—谐波平衡法，以钢丝绳联轴器为例，求出了这类强非线性系统主共振解和次谐共振存在的条件，为避免共振提供了理论依据。
4.用频闪—谐波平衡法和数字仿真比较表明，求得的共振解在定性方面是正确的，在定量方面精度可以满足工程要求。
上一页
下一页
