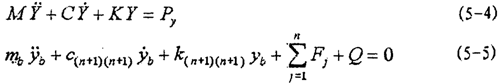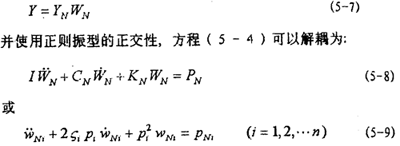第五章 带有非线性联轴器轴系稳态响应计算方法的研究
5-1 带有非线性联轴器轴系力学和数学模型的建立
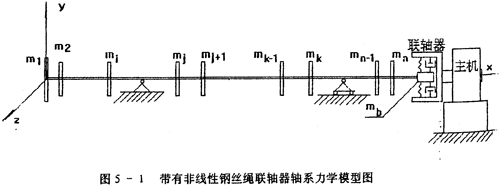
在第三章，根据试验的基础建立了具有非线性迟滞特性联轴器的恢复力模型。这一章，将研究一个带有这种联轴器的轴系如图5-1所示，该轴系有n个圆盘，由钢丝绳联轴器与主机相连接，按以下原则建立力学模型：
1.每个圆盘均视为刚性匀质，所有圆盘的质量mi都有不同程度的偏心距ei。转轴轴线垂直通过各圆盘的几何中心；
2.设轴承、轴承座以及联轴器各向同性，静坐标系如图5-1所示，支座处理成简支；
3.联轴器从动端处理成一集中质量mb，由于联轴器主动端与主机轴相连接，主机轴相对轴系轴来说，较短较粗，刚性较大，变形较小，故将联轴器主动端、主机轴视为一体，位移为零，联轴器从动端与主动端之间由非线性弹簧及非线性阻尼器联结；
4.轴系为小位移振动，且忽略回转效应。
当主机以角速度ω转动时，轴系在各偏心力的作用下产生稳态振动，其运动微分方程可表示为：
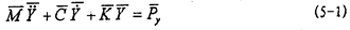
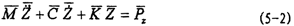
式中
，
，
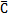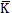，分别为轴系的质量矩阵、阻尼矩阵和刚度矩阵。其中阻尼矩阵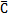=a+b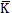，a，b为比例常数。
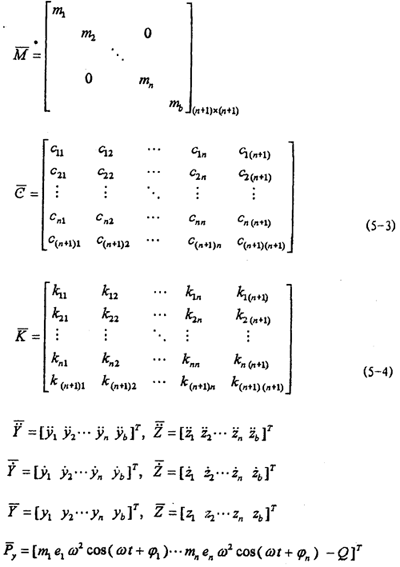
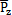=[m1e1ω2sin（ωt+
）…mnenω2sin（ωt+
）
]T
其中：yi,zi分别为轴系中第i个圆盘在y,z方向的位移分量；
i=dyi/dt，
i=d2yi/dt2，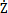
i=dzi/dt，
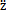b=d2zi/dt2分别为对应于位移分量yi,zi的速度和加速度，yb,zb为联轴器从动端集中质量块mb在y,z方向的位移；b=dyb/dt，b=d2yb/dt2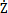，b=dzb/dt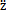，b=d2zb/dt2分别为对应于位移分量yb,zb的速度和加速度；
，
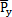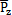为y,z方向的激励力向量，其中mieiω2cos（ωt+
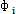），mieiω2sin（ωt+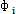）分别为y,z方向的偏心力分量；（
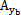，yb，b，ωt),（
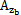，zb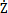，b，ωt）分别为非线性弹性联轴器恢复力在y,z方向的分量。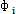为第i个圆盘质量偏心的初相位角，即轴系静止时，第i个圆盘质心和几何中心连线与水平轴的夹角。
由于假设轴承、轴承座以及联轴器各向同性，式（5-1〕、式（5-2）解法相同，只需要讨论二者之一即可。
式（5-l）表示一个局部非线性弹性和阻尼元件的振动系统，对这种系统，按现有常规方法来求解是非常困难的，为此，本文以GILM为基础发展了一种称为SSGILM(Separate System-Gal-erkin and Improved Levenbery-Marquar-dt）的方法来求解此类微分方程组。
5-2 SSGILM法
一.振动微分方程组的改写和解耦
首先把有局部非线性系统振动微分方程组（5-1）式改写成只有线性常系数的微分方程组和一个具有非线性变参数的微分方程两部分：
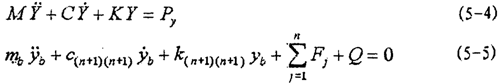
式中：
式（5-4）的Py中含有yb和b而（5-5）的Fj中含有yj，j（j=1，2，… n）。这样，轴系分成运动微分方程耦联的两个子系统—线性轴系子系统和非线性联轴器子系统。
式（5-4）为线性方程，按常规方法可求出无阻尼的各阶固有频率pi以及对应的主振型Yi向量（i=1，2，…，n），Yi分别除以相应广义质量的平方根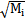
（Mi=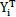
MYi）得到正则振型YNi向量。引入正则振型坐标WNi，对（5-4）式进行坐标变换；
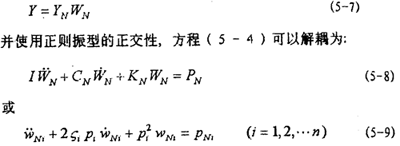
式中，WNi为正则振型向量WN中的第i个分量，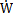
Ni和
Ni，分别为它对时间t的一次导数和二次导数；I为单位矩阵；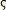
i=（a+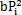
）/2Pi=cii2pimi为振型比例阻尼比；PNi为PN=
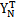Py激励力向量中的第i个分量。
经正则坐标变换，虽然得到互不耦合的线性微分方程组（5-9)，但是（5-9）式仍然不能像单自由度振动系统那样求解，因为（5-9）式中的激励力包含未知的振动位移yb和振动速度b。如果yb已知，就可以从（5-9）式中解得WNi，进而可以由（5-7）式得到各yi。因此需要求得yb。
图5-1所示轴系在主机带动下转动时，各圆盘质量偏心将产生周期偏心激励力，根据第二章的试验结果，联轴器非线性恢复力Q是时间的周期函数，因此当轴系中有联轴器这种局部非线性元件时，可以设它的位移响应是周期性的，即假设yb有下面的形式：
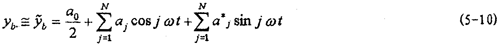
由式（5-6）、（5-8）和（5-9）可知，激励力由二类力构成，一类是质量偏心力mieiω2cos（ωt+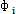），另一类是恢复力-ki（n+1）yb-ci（n+1）b，为求解（5-8）式方便，将（5-10）代入（5-8）式，并将正则激励力分解成：
PN=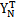Py=PN1+PN2 （5-11）
式中：
由（5-11）和（5-12）式可知，若{a}已知，就可以由（5-12）式求出各WNi，代WNi入（5-7）式，可以得到各yi。由此可以把求yb的问题转化为求{a}=[a0 a1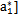 
T的问题。
上一页
下一页
